1 − 2 + 3 − 4 + ⋯

0 + 1 − 2 + 3 − 4 + ning dastlabki 15 000 qismli yigʻindisi … Grafik oʻng tomonda musbat sonlar va chap tomonda manfiy butun sonlar bilan joylashgan.

Matematikada 1 – 2 + 3 – 4 + ··· cheksiz qator boʻlib, hadlari oʻzgaruvchan belgilar berilgan ketma-ket musbat sonlardir. Sigma yigʻindisi yozuvidan foydalanib, qatorning birinchi m hadlarining yigʻindisi quyidagicha ifodalanishi mumkin.

$$\sum _{n=1}^{m}n(-1)^{n-1}.$$

Cheksiz qator ajralib chiqadi, yaʼni uning qisman yigʻindilar ketma-ketligi (1, −1, 2, −2, 3, …) hech qanday chekli chegaraga moyil emas. Shunga qaramay, XVIII asrning oʻrtalarida Leonhard Euler oʻzi tan olgan paradoksal tenglamani yozdi. Leonhard Euler

$$1-2+3-4+\cdots ={\frac {1}{4}}.$$

Ushbu tenglamaning qatʼiy izohi koʻp vaqt oʻtmay keladi. 1890 yildan boshlab Ernesto Sezar, Emile Borel va boshqalar divergent qatorlarga umumlashtirilgan summalarni belgilashning aniq belgilangan usullarini, shu jumladan Eylerning urinishlarining yangi talqinlarini tadqiq qildilar. Ushbu yigʻindilash usullarining koʻpchiligi osongina 1 − 2 + 3 − 4 + …  1/4 „qiymati“ ga tayinlanadi. Sezar yigʻindisi 1 − 2 + 3 — 4 + … ni yigʻmaydigan bir necha usullardan biridir, shuning uchun seriya Abel yigʻindisi kabi biroz kuchliroq usul talab qilinadigan misoldir.

1 − 2 + 3 − 4 + … qatori Grandi 1 − 1 + 1 − 1 + .1 − 1 + 1 − 1 + seriyasi bilan chambarchas bogʻliq. Eyler bu ikkalasini umumiy ketma-ketlikning maxsus holatlari sifatida koʻrib chiqdi. 1 — 2n + 3n — 4n + …, bu erda mos ravishda n = 1 va n = 0. Ushbu tadqiqot yoʻnalishi Bazel muammosi boʻyicha ishini kengaytirdi va hozir Dirichlet eta funktsiyasi va Riemann zeta funktsiyasi deb nomlanuvchi funktsional tenglamalarga olib keldi.

Divergentsiya

Seriya hadlari (1, −2, 3, −4, …) 0 ga yaqinlashmaydi; shuning uchun 1 — 2 + 3 — 4 + … test atamasi boʻyicha farqlanadi. Divergensiyani bevosita taʼrifdan ham koʻrsatish mumkin: cheksiz qator, agar qisman yigʻindilar ketma-ketligi chegaraga yaqinlashsagina yaqinlashadi, bu holda bu chegara cheksiz qatorning qiymati hisoblanadi. 1 − 2 + 3 − 4 + … ning qisman yigʻindilari:

1,

1 − 2 = −1,
1 − 2 + 3 = 2,
1 − 2 + 3 − 4 = −2,
1 − 2 + 3 − 4 + 5 = 3,
1 − 2 + 3 − 4 + 5 − 6 = −3,

...

Qisman yigʻindilar ketma-ketligi qatorning maʼlum bir raqamga yaqinlashmasligini koʻrsatadi: har qanday taklif qilingan x chegarasi uchun, keyingi qisman yigʻindilarning hammasi [x-1, x+1] oraligʻidan tashqarida boʻlgan nuqta mavjud), shuning uchun 1 — 2 + 3 — 4 + … farqlanadi.

Qisman summalar har bir butun sonni bir marta oʻz ichiga oladi, hatto boʻsh qisman yigʻindi hisoblansa ham 0 boʻlsa ham, toʻplamning hisoblanishini oʻrnatadi. $\mathbb {Z}$ butun sonlar.

Jamlash uchun evristika

Barqarorlik va chiziqlilik

1, −2, 3, −4, 5, −6, ... atamalar oddiy sxema boʻyicha kelganligi sababli, 1 − 2 + 3 − 4 + ... qatorlarini haddan tashqari oʻzgartirish va oʻzgartirish orqali boshqarish mumkin. raqamli qiymatni berish uchun qoʻshiladi. Agar baʼzi oddiy s soni uchun s = 1 − 2 + 3 − 4 + ... yozish mantiqiy boʻlsa, quyidagi manipulyatsiyalar s = Andoza:Frac: uchun bahslashadi.

$${\begin{array}{rclllll}4s&=&&(1-2+3-4+\cdots )&{}+(1-2+3-4+\cdots )&{}+(1-2+3-4+\cdots )&{}+(1-2+3-4+\cdots )\\&=&&(1-2+3-4+\cdots )&{}+1+(-2+3-4+5+\cdots )&{}+1+(-2+3-4+5+\cdots )&{}+(1-2)+(3-4+5-6\cdots )\\&=&&(1-2+3-4+\cdots )&{}+1+(-2+3-4+5+\cdots )&{}+1+(-2+3-4+5+\cdots )&{}-1+(3-4+5-6\cdots )\\&=&1+&(1-2+3-4+\cdots )&{}+(-2+3-4+5+\cdots )&{}+(-2+3-4+5+\cdots )&{}+(3-4+5-6\cdots )\\&=&1+[&(1-2-2+3)&{}+(-2+3+3-4)&{}+(3-4-4+5)&{}+(-4+5+5-6)+\cdots ]\\&=&1+[&0+0+0+0+\cdots ]\\4s&=&1\end{array}}$$

1 − 2 + 3 − 4 + ..., faqat siljishlar va muddatlar boʻyicha qoʻshishdan foydalangan holda, 1 ta hosil boʻladi. Chap va oʻng tomonlarning har biri 1 − 2 + 3 − 4 + ... 1 − 1 + 1 − 1 + .... ga qoʻshish. 1 − 2 + 3 − 4 + … ning 4 ta nusxasini qoʻshish, faqat siljishlar va muddatlar boʻyicha qoʻshishdan foydalangan holda, 1 ta hosil boʻladi. Chap va oʻng tomonlarning har biri 1 − 2 + 3 − 4 + ning ikkita nusxasini koʻrsatadi. .. 1 − 1 + 1 − 1 + … ga qoʻshish.

Shunday qilib $s={\frac {1}{4}}$ .

1 − 2 + 3 − 4 + ... odatiy maʼnoda yigʻindiga ega boʻlmasa ham, tenglama s = 1 − 2 + 3 − 4 + ... = Andoza:Frac

1 − 2 + 3 − 4 + … odatiy maʼnoda yigʻindiga ega boʻlmasa ham, s = 1 − 2 + 3 − 4 + … = 1⁄4 tenglamani eng tabiiy javob sifatida qoʻllab-quvvatlash mumkin, agar shunday summa aniqlanishi kerak. Divergent qatorning „yigʻindisi“ning umumlashtirilgan taʼrifi yigʻish usuli yoki yigʻish usuli deb ataladi. Koʻp turli xil usullar mavjud va ular oddiy yigʻishning baʼzi xususiyatlarini baham koʻrishlari maʼqul. Yuqoridagi manipulyatsiyalar aslida quyidagilarni isbotlaydi: chiziqli va barqaror boʻlgan va 1 — 2 + 3 — 4 + … qatorlarini yigʻadigan har qanday yigʻish usulini hisobga olsak, u ishlab chiqaradigan yigʻindi  1⁄4 ga teng.

Bundan tashqari, beri

$${\begin{array}{rcllll}2s&=&&(1-2+3-4+\cdots )&+&(1-2+3-4+\cdots )\\&=&1+{}&(-2+3-4+\cdots )&{}+1-2&{}+(3-4+5\cdots )\\&=&0+{}&(-2+3)+(3-4)+(-4+5)+\cdots \\2s&=&&1-1+1-1\cdots \end{array}}$$

bunday usul Grandi qatorlarini ham 1 − 1 + 1 − 1 + ... = Andoza:Frac. sifatida jamlashi kerak.

bunday usul Grandi qatorlarini ham 1 − 1 + 1 − 1 + … = 1⁄2 sifatida jamlashi kerak.

Cauchy mahsuloti

1891 yilda Ernesto Sesaro divergent qatorlar hisob-kitoblarga qatʼiy kiritilishiga umid bildirdi va shunday taʼkidladi: „Bir kishi allaqachon yozgan (1 − 1 + 1 − 1 + ...)² = 1 − 2 + 3 − 4 + ... va ikkala tomon teng ekanligini taʼkidlaydi 1⁄4“. Sezar uchun bu tenglama u oʻtgan yili eʼlon qilgan teoremaning qoʻllanilishi edi, bu yigʻiladigan divergent qatorlar tarixidagi birinchi teoremadir. Uning yigʻish usuli haqida batafsil maʼlumot quyida keltirilgan; markaziy fikr shundan iboratki, 1 − 2 + 3 − 4 + ... 1 − 1 + 1 − 1 + ... ning 1 − 1 + 1 − 1 + ... bilan Koshi mahsuloti (diskret konvolyutsiya) hisoblanadi. 1 − 1 + 1 − 1 + ... 1 − 1 + 1 − 1 + ... .

Ikki cheksiz qatorning Koshi mahsuloti, hatto ularning har ikkalasi bir-biridan farq qilganda ham aniqlanadi. a _n = b _n = (−1) ⁿ boʻlgan holatda, Koshi mahsulotining shartlari chekli diagonal yigʻindilar bilan beriladi.

$${\begin{array}{rcl}c_{n}&=&\displaystyle \sum _{k=0}^{n}a_{k}b_{n-k}=\sum _{k=0}^{n}(-1)^{k}(-1)^{n-k}\\[1em]&=&\displaystyle \sum _{k=0}^{n}(-1)^{n}=(-1)^{n}(n+1).\end{array}}$$

Mahsulot seriyasi keyin

$$\sum _{n=0}^{\infty }(-1)^{n}(n+1)=1-2+3-4+\cdots .$$

Shunday qilib, ikki qatorning Koshi mahsulotini hurmat qiladigan yigʻindi usuli — va 1 − 1 + 1 − 1 + ... qatorga 1/2 yigʻindini belgilaydi — 1 − 2 + 3 − 4 + ... summasi 1/4. Oldingi boʻlimning natijasi bilan, bu chiziqli, barqaror va Koshiga rioya qiladigan usullar bilan 1 − 1 + 1 − 1 + ... va 1 − 2 + 3 − 4 + ... yigʻindisi oʻrtasidagi ekvivalentlikni nazarda tutadi. mahsulot.

Sezar teoremasi nozik misoldir. 1 − 1 + 1 − 1 + ... qatori eng zaif maʼnoda Sezar yigʻiladigan, (C, 1)-summable, 1 − 2 + 3 − 4 + ... esa Sezar teoremasining kuchliroq shaklini talab qiladi., boʻlish (C, 2)-summable. Sezar teoremasining barcha shakllari chiziqli va barqaror boʻlgani uchun yigʻindilarning qiymatlari yuqorida hisoblangandek boʻladi.

Maxsus usullar

Sezar va Xölder

1⁄4 ning (H, 2) yigʻindisi haqidagi maʼlumotlar

1 − 2 + 3 − 4 + … ning (C, 1) Sezar yigʻindisini topish uchun, agar u mavjud boʻlsa, qatorning qisman yigʻindilarining arifmetik vositalarini hisoblash kerak. Qisman summalar:.

1, −1, 2, −2, 3, −3, ...,

va bu qisman summalarning arifmetik vositalari:

1, 0, Andoza:Frac, 0, Andoza:Frac, 0, Andoza:Frac, ….

Ushbu vositalar ketma-ketligi yaqinlashmaydi, shuning uchun 1 − 2 + 3 − 4 + … Cesàro yigʻindisi emas.

Sezar yigʻindisining ikkita mashhur umumlashmasi mavjud: ulardan kontseptual jihatdan soddaroqsi n natural sonlar uchun (H, n) usullarning ketma-ketligidir. (H, 1) yigʻindisi Sezar yigʻindisidir va yuqoriroq usullar vositalarni hisoblashni takrorlaydi. Yuqorida juft maʼnolari yaqinlashadi1⁄2 boʻlsa, toq oʻrtachalarning barchasi 0 ga teng, shuning uchun vositalarning vositalari oʻrtacha 0 ga yaqinlashadi va1⁄2, yaʼni1⁄4 . Demak, 1 − 2 + 3 − 4 + ... (H, 2) ga yigʻiladi1⁄4 .

„H“ harfi Otto Xolderni anglatadi, u birinchi marta 1882 yilda matematiklar Abel yigʻindisi va (H, n) yigʻindisi oʻrtasidagi bogʻliqlik deb oʻylashlarini isbotlagan; 1 − 2 + 3 − 4 + ... uning birinchi misoli edi. Gap shundaki1⁄4 1 − 2 + 3 − 4 + ... ning (H, 2) yigʻindisi, uning ham Abel yigʻindisi ekanligini kafolatlaydi; Bu ham quyida toʻgʻridan-toʻgʻri isbotlanadi.

Sezar yigʻindisining yana bir keng tarqalgan umumlashmasi (C, n) usullarining ketma-ketligidir. (C, n) yigʻindisi va (H, n) yigʻindisi har doim bir xil natija berishi isbotlangan, lekin ularning tarixiy asoslari har xil. 1887 yilda Sesaro (C, n) yigʻindisining taʼrifini aytishga yaqin keldi, lekin u bir nechta misollar keltirdi. Xususan, u 1 − 2 + 3 − 4 + ..., to ni jamlagan1⁄4 (C, n) deb qayta ifodalanishi mumkin boʻlgan, ammo oʻsha paytda oqlanmagan usul bilan. U 1890 yilda (C, n) yigʻiladigan qator va (C, m) yigʻiladigan qatorlarning Koshi koʻpaytmasi (C, m + n +) ekanligi haqidagi teoremasini bayon qilish uchun (C, n) usullarini rasman belgilab berdi. 1) — yigʻiladigan.

Abel yigʻindisi

1 − 2x + 3x² + … ning baʼzi qismlari; 1/(1 + x)²; va chegaralar 1 ga teng

1749-yilgi hisobotda Leonhard Eyler seriyalar bir-biridan farq qilishini tan oladi, ammo baribir uni umumlashtirishga tayyor:

... when it is said that the sum of this series 1 − 2 + 3 − 4 + 5 − 6 etc. is Andoza:Frac, that must appear paradoxical. For by adding 100 terms of this series, we get −50, however, the sum of 101 terms gives +51, which is quite different from Andoza:Frac and becomes still greater when one increases the number of terms. But I have already noticed at a previous time, that it is necessary to give to the word sum a more extended meaning …

Eyler bir necha marta „sum“ soʻzini umumlashtirishni taklif qildi. 1 − 2 + 3 − 4 + ... boʻlsa, uning gʻoyalari hozirgi Abel yigʻindisi deb ataladigan narsaga oʻxshaydi:

... it is no more doubtful that the sum of this series 1 − 2 + 3 − 4 + 5 etc. is Andoza:Frac; since it arises from the expansion of the formula Andoza:Frac, whose value is incontestably Andoza:Frac. The idea becomes clearer by considering the general series 1 − 2x + 3x² − 4x³ + 5x⁴ − 6x⁵ + &c. that arises while expanding the expression Andoza:Frac, which this series is indeed equal to after we set x = 1.

Buni koʻrishning koʻplab usullari mavjud, hech boʻlmaganda mutlaq qiymatlar uchun Andoza:Abs < 1, Eyler bu borada haqliFailed to parse (sintaktik xato): {\displaystyle 1-2x+3x²-4x³+\cdots = \frac{1}{(1+x)²}.} Oʻng tomonning Teylor kengaytmasini olish mumkin yoki koʻphadlar uchun rasmiy uzun boʻlinish jarayonini qoʻllash mumkin. Chap tomondan boshlab, yuqoridagi umumiy evristikaga amal qilib, (1 + x) ga ikki marta koʻpaytirishga yoki 1 − x + x² − ... geometrik qatorni kvadratga olishga harakat qilish mumkin. 1 − x + x² − ... 1 − x + x² − ... . Eyler, shuningdek, oxirgi turkum atamalarini atama boʻyicha farqlashni taklif qilganga oʻxshaydi.

Zamonaviy koʻrinishda 1 — 2 x + 3 x ² — 4 x ³ + … hosil qiluvchi funktsiya x = 1 da funktsiyani aniqlamaydi, shuning uchun qiymatni natijada olingan ifodaga oddiygina almashtirib boʻlmaydi. Funktsiya hamma uchun aniqlanganligi uchun |x| < 1, x 1 ga yaqinlashganda ham chegarani olish mumkin va bu Abel summasining taʼrifi:

Failed to parse (sintaktik xato): {\displaystyle \lim_{x\rightarrow 1^{-}}\sum_{n=1}^\infty n(-x)^{n-1} = \lim_{x\rightarrow 1^{-}}\frac{1}{(1+x)²} = \frac14.}

Eyler va Borel

Eyler yigʻindisi 1⁄2 −1⁄4 . Ijobiy qiymatlar oq rangda, salbiy qiymatlar jigarrang rangda, siljishlar va bekor qilishlar yashil rangda koʻrsatilgan.

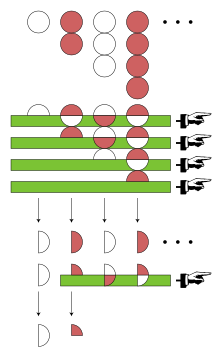
Eyler seriyaga boshqa texnikani qoʻlladi: Eyler transformatsiyasi, oʻzining ixtirolaridan biri. Eyler konvertatsiyasini hisoblash uchun oʻzgaruvchan qatorni tashkil etuvchi musbat hadlar ketma-ketligidan boshlanadi — bu holda 1, 2, 3, 4, .... 1, 2, 3, 4, .... 1, 2, 3, 4, .... 1, 2, 3, 4, .... Ushbu ketma-ketlikning birinchi elementi ₀ bilan belgilanadi.

Keyin 1, 2, 3, 4, ... orasidagi toʻgʻridan-toʻgʻri farqlar ketma-ketligi kerak; bu faqat 1, 1, 1, 1, .... 1, 1, 1, 1, .... 1, 1, 1, 1, .... 1, 1, 1, 1, .... Ushbu ketma-ketlikning birinchi elementi D a ₀ bilan belgilanadi. Eyler konvertatsiyasi ham farqlar farqiga va yuqori iteratsiyalarga bogʻliq, ammo 1, 1, 1, 1, ... oʻrtasidagi barcha toʻgʻridan-toʻgʻri farqlar 0 ga teng. 1 − 2 + 3 − 4 + ... Eyler konvertatsiyasi quyidagicha aniqlanadi

Failed to parse (sintaktik xato): {\displaystyle \frac12 a_0-\frac14\Delta a_0 +\frac18\Delta² a_0 -\cdots = \frac12-\frac14.} Zamonaviy terminologiyada aytilishicha, 1 − 2 + 3 − 4 + ... Eylerning yigʻindisi hisoblanadi.1⁄4 .

Eyler yigʻindisi ham umumiy boʻlgani kabi bir xil yigʻindi qiymatiga ega Borel yigʻindisini ham nazarda tutadi.

Tarozilarni ajratish

Saichev va Voychiński 1 − 2 + 3 − 4 + ... = Andoza:Frac da kelishadi.

Bu natija φ (x) = exp(− x) ga ruxsat berish orqali tiklanadigan Abel yigʻindisini umumlashtiradi. Umumiy fikr ketma-ketlikdagi hadlarni m dan ortiq juftlash va ifodani Riman integraliga aylantirish orqali isbotlanishi mumkin. Oxirgi bosqich uchun 1 − 1 + 1 − 1 + ... uchun mos keladigan dalil oʻrtacha qiymat teoremasini qoʻllaydi, ammo bu erda Teylor teoremasining kuchliroq Lagrange shakli kerak.

• Agar φ (x) birinchi va ikkinchi hosilalari uzluksiz va (0, ∞) ustida integrallanadigan funksiya boʻlsa, ph(0) = 1 va ph(x) va x ph(x) ning +∞ da chegaralari boʻlsin. ikkalasi ham 0, keyin
  $$\lim _{\delta \rightarrow 0}\sum _{m=0}^{\infty }(-1)^{m}(m+1)\varphi (\delta m)={\frac {1}{4}}.$$

Bu natija Abel yigʻindisini umumlashtiradi, u ph(x) = exp(−x) ga ruxsat berish orqali tiklanadi. Umumiy fikrni qatordagi hadlarni m dan ortiq juftlash va ifodani Riman integraliga aylantirish orqali isbotlash mumkin. Oxirgi bosqich uchun 1 — 1 + 1 — 1 + uchun mos dalil. oʻrtacha qiymat teoremasini qoʻllaydi, lekin bu erda Teylor teoremasining kuchliroq Lagrange shakli kerak.

Umumlashtirish

betdan parcha. E212 ning 233— Institutiones calculi differentialis cum eius us to analysis in the end of doctrina serierum . Eyler shunga oʻxshash qatorlarni jamlaydi, tax. 1755 .

1 − 1 + 1 − 1 + ... ning uch karrali Koshi koʻpaytmasi 1 − 3 + 6 − 10 + ..., uchburchak sonlarning oʻzgaruvchan qatori; uning Abel va Eyler yigʻindisi 1⁄8. 1 − 1 + 1 − 1 + ... ning toʻrt karra Koshi koʻpaytmasi 1 − 4 + 10 − 20 + ..., tetraedral sonlarning oʻzgaruvchan qatori, Abel yigʻindisi 1⁄16.

1 — 2 + 3 — 4 + … biroz boshqacha yoʻnalishdagi yana bir umumlashma n ning boshqa qiymatlari uchun 1 − 2ⁿ + 3ⁿ − 4ⁿ + ... qatoridir. Musbat butun sonlar uchun n, bu qatorlar quyidagi Abel yigʻindilariga ega:

$$1-2^{n}+3^{n}-\cdots ={\frac {2^{n+1}-1}{n+1}}B_{n+1}$$

Bu yerda B_n — Bernoulli raqamlari. Hatto n uchun bu ga kamayadi

$$1-2^{2k}+3^{2k}-\cdots =0,$$

Riemann zeta funksiyasining manfiy juft qiymatlari nolga teng deb talqin qilish mumkin. Bu summa 1826-yilda Niels Henrik Abel tomonidan alohida masxara ob’ektiga aylandi:

Divergent series are on the whole devil's work, and it is a shame that one dares to found any proof on them. One can get out of them what one wants if one uses them, and it is they which have made so much unhappiness and so many paradoxes. Can one think of anything more appalling than to say that

0 = 1 − 2²ⁿ + 3²ⁿ − 4²ⁿ + etc.

where n is a positive number. Hereʼs something to laugh at, friends.

Sezarning oʻqituvchisi Ejen Charlz Katalan ham bir-biridan farq qiluvchi seriyalarni yomon koʻrdi. Kataloniya taʼsiri ostida Sezar dastlab 1 − 2ⁿ + 3ⁿ − 4ⁿ + ... uchun „anʼanaviy formulalar“ ni „bemaʼni tenglik“ deb atagan va 1883 yilda Sezar formulalar notoʻgʻri ekanligi haqidagi odatiy fikrni bildirgan. lekin baribir qandaydir rasmiy ravishda foydali. Nihoyat, 1890-yilda "Sur la multiplication des séries" asarida Sesaro taʼriflardan boshlab zamonaviy yondashuvni qoʻlladi.

Seriya n ning butun boʻlmagan qiymatlari uchun ham oʻrganiladi; Bular Dirichlet eta funksiyasini tashkil qiladi. Eylerning 1 − 2 + 3 − 4 + ... bilan bogʻliq qatorlarni oʻrganish motivatsiyasining bir qismi eta funktsiyasining funktsional tenglamasi boʻlib, bu toʻgʻridan-toʻgʻri Riemann zeta funktsiyasining funktsional tenglamasiga olib keladi. Eyler allaqachon bu funksiyalarning qiymatlarini musbat juft sonlarda (jumladan , Bazel muammosi) topish bilan mashhur boʻlgan va u musbat toq sonlardagi qiymatlarni (jumladan , Aperi doimiysi) topishga harakat qilgan, bugungi kunda bu muammoni hal qilish qiyin. . Ayniqsa, eta funksiyasini Eyler usullari bilan hal qilish osonroq, chunki uning Dirichlet seriyasi hamma joyda Abel yigʻindisidir; zeta funktsiyasining Dirichlet qatorini uning ajralish joyini yigʻish ancha qiyin. Masalan, zeta funksiyasidagi 1 − 2 + 3 − 4 + ... oʻxshashi oʻzgaruvchan boʻlmagan 1 + 2 + 3 + 4 + ... qator boʻlib, u zamonaviy fizikada chuqur ilovalarga ega, lekin ancha kuchliroq talablarni talab qiladi. jamlash usullari.

Yana qarang

• 1 + 2 + 3 + 4 + ⋯
• 1 + 1 + 1 + 1 + ⋯
• 1 + 2 + 4 + 8 + ·. . .
• 1 − 2 + 4 − 8 + ⋯

Adabiyotlar

• Alabdulmohsin, Ibrahim M. „Analytic summability theory“,. Summability Calculus. Springer International Publishing, 2018 — 65–91 bet. DOI:10.1007/978-3-319-74648-7_4. ISBN 978-3-319-74647-0. 
• Beals, Richard. Analysis: An Introduction. Cambridge UP, 2004. ISBN 978-0-521-60047-7. 
• Davis, Harry F.. Fourier Series and Orthogonal Functions. Dover, May 1989. ISBN 978-0-486-65973-2. 
• Euler, Leonhard; Willis, Lucas; Osler, Thomas J. „Translation with notes of Euler's paper: Remarks on a beautiful relation between direct as well as reciprocal power series“. The Euler Archive (2006). Qaraldi: 2007-yil 22-mart.

• Originally published as Euler, Leonhard (1768). "Remarques sur un beau rapport entre les séries des puissances tant directes que réciproques". Mémoires de l'Académie des Sciences de Berlin 17: 83–106. 
• Ferraro, Giovanni (June 1999). "The First Modern Definition of the Sum of a Divergent Series: An Aspect of the Rise of 20th Century Mathematics". Archive for History of Exact Sciences 54 (2): 101–135. doi:10.1007/s004070050036. 
• Grattan-Guinness, Ivor. The development of the foundations of mathematical analysis from Euler to Riemann. MIT Press, 1970. ISBN 978-0-262-07034-8. 
• Hardy, G. H.. Divergent Series. Clarendon Press, 1949 — xvi+396 bet. ISBN 978-0-8218-2649-2. OCLC 808787.  2nd Ed. published by Chelsea Pub. Co., 1991. Andoza:LCCN. ISBN 0-8284-0334-1.
• Kline, Morris (November 1983). "Euler and Infinite Series". Mathematics Magazine 56 (5): 307–314. doi:10.2307/2690371. https://archive.org/details/sim_mathematics-magazine_1983-11_56_5/page/307. 
• Knopp, Konrad. Theory and Application of Infinite Series. New York: Dover Publications, 1990. ISBN 0486661652. 
• Lavine, Shaughan. Understanding the Infinite. Harvard UP, 1994. ISBN 978-0-674-92096-5. 
• Markusevič, Aleksej Ivanovič. Series: fundamental concepts with historical exposition, English translation of 3rd revised edition (1961) in Russian, Delhi, India: Hindustan Pub. Corp., 1967 — 176 bet. OCLC 729238507.  Author also known as A. I. Markushevich and Alekseï Ivanovitch Markouchevitch. Also published in Boston, Mass by Heath with Andoza:Oclc. Additionally, Andoza:Oclc, Andoza:Oclc.
• Saichev, A. I.; Woyczyński, W. A.. Distributions in the Physical and Engineering Sciences, Volume 1. Birkhaüser, 1996. ISBN 978-0-8176-3924-2. 
• Shawyer, Bruce; Watson, Bruce. Borel's Methods of Summability: Theory and Application, Oxford Mathematical Monographs. The Clarendon Press, Oxford University Press, New York, 1994. ISBN 0-19-853585-6. 
• Tucciarone, John (January 1973). "The development of the theory of summable divergent series from 1880 to 1925". Archive for History of Exact Sciences 10 (1–2): 1–40. doi:10.1007/BF00343405. 
• Vretblad, Anders. Fourier Analysis and Its Applications. Springer, 2003. ISBN 978-0-387-00836-3.