Laplas-Runge-Lenz vektori: Versiyalar orasidagi farq

Kontent oʻchirildi Kontent qoʻshildi

Inline

10-Avgust 2023, 17:15 dagi koʻrinishi

Klassik mexanikada Laplas-Runge-Lenz (LRL) vektori asosan bir astronomik jismning boshqasi atrofidagi orbitasining shakli va yo'nalishini, masalan, qo'shaloq yulduz yoki yulduz atrofida aylanadigan sayyorani tasvirlash uchun ishlatiladigan vektordir . Nyuton tortishish kuchi bilan o'zaro ta'sir qiluvchi ikkita jism uchun LRL vektori harakat doimiysi bo'lib, u orbitaning qayerda hisoblanganidan qat'i nazar, bir xil bo'ladi^[1] ^[2]; ekvivalenti LRL vektori saqlanuvchi deyiladi. Umuman olganda, LRL vektori ikkita jismning o'zaro ta'sirida ular orasidagi masofaning teskari kvadrati sifatida o'zgarib turadigan markaziy kuch bilan o'zaro ta'sir qiladigan barcha masalalarda saqlanadi; bunday muammolar Kepler muammolari deb ataladi^[3] ^[4] ^[5] ^[6].

Vodorod atomi Kepler muammosidir, chunki u Kulonning elektrostatika qonuni bo'yicha o'zaro ta'sir qiluvchi ikkita zaryadlangan zarrachani o'z ichiga oladi, bu boshqa teskari kvadrat markaziy kuch. LRL vektori Shredinger tenglamasi ishlab chiqilishidan oldin vodorod atomi spektrining birinchi kvant mexanik hosilasida muhim ahamiyatga ega edi^[7] ^[8]. Biroq, bugungi kunda bu yondashuv kamdan-kam qo'llaniladi.

Klassik va kvant mexanikasida saqlanib qolgan miqdorlar odatda sistemaning simmetriyasiga mos keladi^[9]. LRL vektorining saqlanishi noodatiy simmetriyaga mos keladi; Kepler muammosi to'rt o'lchovli (giper-)sfera yuzasida erkin harakatlanadigan zarrachaga matematik jihatdan ekvivalentdir ^[10], shuning uchun butun muammo to'rt o'lchovli fazoning ma'lum aylanishlari ostida simmetrik bo'ladi^[11]. Bu yuqori simmetriya Kepler muammosining ikkita xususiyatidan kelib chiqadi: tezlik vektori har doim mukammal aylana bo'ylab harakat qiladi va berilgan umumiy energiya uchun barcha tezlik doiralari bir xil ikkita nuqtada bir-birini kesib o'tadi^[12].

Laplas-Runge-Lenz vektori Per-Simon de Laplas, Karl Rung va Vilgelm Lents sharafiga nomlangan. U Laplas vektori^[13] ^[14], Runge-Lenz vektori va Lenz vektori sifatida ham tanilgan^[15] ^[8]. Qizig'i shundaki, o'sha olimlarning hech biri buni kashf etmagan^[15]. LRL vektori bir necha marta qayta kashf etilgan va qayta tuzilgan^[15]; masalan, samoviy mexanikaning o'lchovsiz ekssentriklik vektoriga ekvivalentdir^[2] ^[14] ^[16]. LRL vektorining turli umumlashtirishlari aniqlangan, ular maxsus nisbiylik, elektromagnit maydonlar va hatto turli xil markaziy kuchlarning ta'sirini o'z ichiga oladi^[17] ^[18] ^[19].

Nazariy qismi

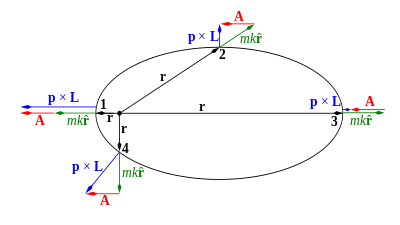
Har qanday konservativ markaziy kuch ostida harakatlanadigan bitta zarracha kamida to'rtta doimiy harakatga ega: umumiy energiya $E$ va kuch markaziga nisbatan burchak momentum vektori $L$ ning uchta dekart komponenti^[20] ^[21]. Zarrachaning orbitasi zarrachaning dastlabki impulsi $p$ (yoki ekvivalenti uning tezligi $v$ ) va zarracha bilan kuch markazi oʻrtasidagi vektor $r$ bilan aniqlangan tekislik bilan chegaralangan (1-rasmga qarang)^[20] ^[21]. Bu harakat tekisligi doimiy burchak momentum vektoriga perpendikulyar $L = r \times p$ ; bu vektor nuqta mahsulot tenglamasi bilan matematik tarzda ifodalanishi mumkin $r \cdot L = 0$ . Quyida uning matematik ta’rifini hisobga olsak, Laplas–Runge–Lenz vektori (LRL vektor) $A$ barcha markaziy kuchlar uchun doimo doimiy burchak momentum vektori $L$ ga perpendikulyar bo‘ladi ( $A \cdot L = 0$ ). Shuning uchun $A$ har doim harakat tekisligida yotadi. Quyida ko'rsatilgandek, $A$ kuch markazidan harakatning periapsisiga, eng yaqin yaqinlashish nuqtasiga va uning uzunligi orbitaning eksantrikligiga proportsionaldir^[1].

LRL vektor $A$ uzunligi va yo'nalishi bo'yicha doimiy, lekin faqat teskari kvadrat markaziy kuch uchun^[1]. Boshqa markaziy kuchlar uchun $A$ vektor doimiy emas, balki uzunligi va yo'nalishi bo'yicha o'zgaradi. Agar markaziy kuch taxminan teskari kvadrat qonuni bo'lsa, $A$ vektor uzunligi bo'yicha taxminan doimiy, lekin asta-sekin o'z yo'nalishini aylantiradi^[14]. Umumiy saqlangan LRL vektori ${\mathcal {A}}$ barcha markaziy kuchlar uchun aniqlanishi mumkin, ammo bu umumlashtirilgan vektor pozitsiyaning murakkab funktsiyasidir va odatda yopiq shaklda ifodalanmaydi^[18] ^[19].

Qayta kashf qilish tarixi

LRL vektor $A$ Kepler muammosining harakat doimiysi bo'lib, sayyoralar va qo'shaloq yulduzlar harakati kabi astronomik orbitalarni tavsiflashda foydalidir. Shunga qaramay, u fiziklar orasida hech qachon yaxshi ma'lum bo'lmagan, ehtimol u momentum va burchak momentumidan kamroq intuitivdir. Binobarin, so'nggi uch asr davomida u bir necha marta mustaqil ravishda qayta kashf etilgan^[15].

Yakob Hermann birinchi bo'lib $A$ teskari kvadrat markaziy kuchning maxsus holati uchun saqlanishini ko'rsatdi va uning orbital ellipsning ekssentrisiteti bilan bog'lanishini ishlab chiqdi^[22]. Hermannning ishi 1710 yilda Iogan Bernulli tomonidan zamonaviy shaklga umumlashtirildi ^[23]. Asrning oxirida Per-Simon de Laplas $A$ ning saqlanishini qayta kashf etdi va uni geometrik emas, balki analitik tarzda keltirib chiqardi^[24]. O'n to'qqizinchi asr o'rtalarida Uilyam Rouen Gamilton quyida aniqlangan ekvivalent ekssentriklik vektorini chiqardi va undan foydalanib impuls vektori $p$ aylana bo'ylab teskari kvadrat markaziy kuch ta'sirida harakat qilishini ko'rsatdi (3-rasm)^[16] ^[12].

Yigirmanchi asrning boshida Josiah Willard Gibbs vektor tahlili orqali xuddi shu vektorni oldi^[25]. Gibbsning hosilasi misol sifatida Karl Runge tomonidan vektorlar bo'yicha mashhur nemis darsligida ishlatilgan ^[26], Vilgelm Lenz vodorod atomining (eski) kvant mexanik ishlovi haqidagi maqolasida unga havola qilingan^[27]. 1926 yilda Volfgang Pauli LRL vektoridan vodorod atomining energiya darajalarini kvant mexanikasining matritsa mexanikasi formulasidan foydalangan holda LRLni olish uchun ishlatgan^[7], shundan so'ng u asosan Runge-Lenz vektori sifatida tanilgan^[15].

Matematik ta'rif

Bitta zarrachaga ta'sir etuvchi teskari kvadrat markaziy kuch tenglama bilan tavsiflanadi

\mathbf {F} (r)=-{\frac {k}{r^{2}}}\mathbf {\hat {r}} ;

Tegishli potensial energiya tomonidan berilgan $V(r)=-k/r$ . Doimiy parametr $k$ markaziy kuchning kuchini tavsiflaydi; tortishish kuchi uchun $G \cdot M \cdot m$ va elektrostatik kuchlar uchun $- k e \cdot Q \cdot q$ ga teng. Agar $k > 0$ bo'lsa, kuch jozibador, agar $k < 0$ bo'lsa, itaruvchi.

LRL vektor $A$ matematik tarzda formula bilan aniqlanadi^[1].Andoza:Equation box 1jadval-1

bu yerda

$m$ markaziy kuchlar natijasida harakatlangan zarrachaningmassasi,
$L = r \times p$ burchak momenti vektori,
$r$ zarrachaning koordinata vektori (1-rasm),
$\mathbf {\hat {r}}$ birlik vektor, masalan, $\mathbf {\hat {r}} ={\frac {\mathbf {r} }{r}}$ ,
$r$ - $r$ ning miqdor kattaligi, markaziy kuchdan zarrachagacha bo'lgan masofa.

LRL vektorining SI birliklari joule-kilogramm (J⋅kg⋅m) dir. Buning sababi, $p$ va $L$ ning birliklari mos ravishda kg⋅m/s va J⋅s. Bu $m$ (kg) va $k$ (N⋅m ² ) birliklariga mos keladi.

LRL $A$ vektorining bu ta'rifi qattiq kuch ta'sirida harakatlanayotgan $m$ massali bir nuqtali zarrachaga tegishli. Shu bilan birga, xuddi shu ta'rifni Kepler muammosi kabi ikki jismli muammolarga, $m$ ikki jismning kamaytirilgan massasi va $r$ ikki jism orasidagi vektor sifatida qabul qilish orqali kengaytirish mumkin.

Qabul qilingan kuch konservativ bo'lganligi sababli, umumiy energiya $E$ harakat doimiysi,

E={\frac {p^{2}}{2m}}-{\frac {k}{r}}={\frac {1}{2}}mv^{2}-{\frac {k}{r}}.

Qabul qilingan kuch ham markaziy kuchdir. Demak, burchak momentum vektori

L

ham saqlanib qoladi va zarracha harakatlanadigan tekislikni belgilaydi. LRL vektor

A

burchak momentum vektori

L

ga perpendikulyar, chunki

p \times L

va

r

ikkala

L

ga perpendikulyar. Bundan kelib chiqadiki,

A

harakat tekisligida yotadi.

Harakatning bir xil doimiyligi uchun muqobil formulalar, odatda vektorni massa $m$ , kuch parametri $k$ yoki burchak momentum $L$ kabi doimiylar bilan masshtablash orqali aniqlanishi mumkin^[15]. Eng keng tarqalgan variant $A$ ni $mk$ ga bo‘lishdir, bu ekssentriklik vektorini beradi moduli konusning ekssentrisitetiga teng bo‘lgan yarim katta o‘q bo‘ylab o‘lchamsiz vektor^[2] ^[16]:

\mathbf {e} ={\frac {\mathbf {A} }{mk}}={\frac {1}{mk}}(\mathbf {p} \times \mathbf {L} )-\mathbf {\hat {r}} .

Ekvivalent formula bu ekssentriklik vektorini katta yarim o'q

a

ga ko'paytiradi^[14], natijada vektor uzunlik birliklarini beradi. Yana bir formula

A

ga ajratadi

L^{2}

^[28], teskari uzunlik birliklari bilan ekvivalent saqlangan miqdorni beradi, bu miqdor Kepler muammosini hal qilishda paydo bo'ladi.

u\equiv {\frac {1}{r}}={\frac {km}{L^{2}}}+{\frac {A}{L^{2}}}\cos \theta

bu yerda

\theta

-

A

va pozitsiya vektori

r

orasidagi burchak. Qo'shimcha muqobil formulalar quyida keltirilgan.

Kepler orbitalarining kelib chiqishi

Orbitalarning shakli va orientatsiyasini LRL vektoridan quyidagicha aniqlash mumkin^[1]. $A$ ning nuqta ko'paytmasini $r$ pozitsiya vektori bilan olib, tenglama hosil bo'ladi

\mathbf {A} \cdot \mathbf {r} =A\cdot r\cdot \cos \theta =\mathbf {r} \cdot \left(\mathbf {p} \times \mathbf {L} \right)-mkr,

bu yerda $θ$ - $r$ va $A$ orasidagi burchak (2-rasm). Skayar uchlik mahsulot rentabelligini almashtirish

\mathbf {r} \cdot \left(\mathbf {p} \times \mathbf {L} \right)=\left(\mathbf {r} \times \mathbf {p} \right)\cdot \mathbf {L} =\mathbf {L} \cdot \mathbf {L} =L^{2}

Qayta tartiblash Kepler tenglamasining yechimini beradiAndoza:Equation box 1jadval-2

Bu ekssentriklik e ning konus kesimi formulasiga mos keladi

{\frac {1}{r}}=C\cdot \left(1+e\cdot \cos \theta \right)

bu yerda ekssentriklik

e={\frac {A}{\left|mk\right|}}\geq 0

va

C

doimiydir^[1].

$A$ ning nuqta mahsulotini o‘zi bilan olib, umumiy energiya $E$ o‘z ichiga olgan tenglama hosil bo‘ladi^[1].

A^{2}=m^{2}k^{2}+2mEL^{2},

ekssentriklik nuqtai nazaridan qayta yozilishi mumkin^[1].

e^{2}=1+{\frac {2L^{2}}{mk^{2}}}E.

Shunday qilib, agar energiya

E

manfiy bo'lsa (bog'langan orbitalar), ekssentriklik birdan kichik va orbita ellipsdir. Aksincha, energiya ijobiy bo'lsa (bog'lanmagan orbitalar, "tarqalgan orbitalar" deb ham ataladi)^[1], ekssentriklik birdan katta va orbita giperbola bo'ladi^[1]. Nihoyat, agar energiya aniq nolga teng bo'lsa, eksantriklik bitta va orbita parabola bo'ladi^[1]. Barcha holatlarda

A

yo'nalishi konus kesimining simmetriya o'qi bo'ylab yotadi va kuch markazidan periapsisga, eng yaqin yaqinlashish nuqtasiga ishora qiladi^[1].

Harakat va superintegratsiya konstantalari

Yetti skalyar miqdorlar $E$ , $A$ va $L$ (vektor boʻlib, oxirgi ikkitasi har biri uchta saqlangan miqdorga hissa qoʻshadi) ikkita tenglama bilan bogʻlangan, $A \cdot L = 0$ va $A 2 = m 2 k 2 + 2 mEL 2$ , beshta mustaqil konstantani beradi. harakatdan . ( $A$ ning kattaligi, demak, orbitaning ekssentrisiteti $e$ umumiy burchak impulsi $L$ va $E$ energiyasidan aniqlash mumkin bo'lganligi sababli, faqat $A$ ning yo'nalishi mustaqil ravishda saqlanadi; bundan tashqari, $A$ $L$ ga perpendikulyar bo'lishi kerakligi sababli, u hissa qo'shadi. faqat bitta qo'shimcha saqlangan miqdor. )

Bu zarrachaning orbitasini belgilaydigan oltita boshlang'ich shartga (zarrachaning boshlang'ich holati va tezlik vektorlari, har biri uchta komponentdan iborat) mos keladi, chunki boshlang'ich vaqt harakat konstantasi bilan aniqlanmaydi. Shunday qilib, 6 o'lchovli fazali fazodagi 1 o'lchovli orbita to'liq aniqlangan.

Erkinlik darajasi $d$ bo'lgan mexanik tizim ko'pi bilan $2 d - 1$ harakat konstantasiga ega bo'lishi mumkin, chunki 2 d boshlang'ich shartlar mavjud va boshlang'ich vaqtni harakat konstantasi bilan aniqlab bo'lmaydi. Harakat konstantalari $d$ dan ortiq bo'lgan tizim superintegral, $2 d - 1$ konstantaga ega bo'lgan tizim maksimal superintegral deb ataladi^[29]. Gamilton-Jakobi tenglamasini bitta koordinata tizimida yechish faqat $d$ harakat konstantasini berishi mumkinligi sababli, superintegratsiyalanuvchi tizimlar bir nechta koordinatalar tizimida ajratilishi kerak^[30]. Kepler muammosi maksimal darajada superintegraldir, chunki u uchta erkinlik darajasiga ( $d = 3$ ) va besh mustaqil harakat doimiysiga ega; uning Gamilton-Jakobi tenglamasi quyida tavsiflanganidek sferik koordinatalarda ham, parabolik koordinatalarda ham ajratilishi mumkin^[17].

Maksimal superintegratsiyalanadigan tizimlar fazalar fazosida yopiq, bir o'lchovli orbitalarni kuzatib boradilar, chunki orbita ularning harakat konstantalarining fazo-fazo izoyuzalarining kesishishi hisoblanadi. Binobarin, orbitalar ushbu barcha mustaqil izo-sirtlarning barcha gradientlariga perpendikulyar bo'lib, ushbu maxsus muammoda beshtasi mavjud va shuning uchun bu barcha gradientlarning umumlashtirilgan ko'ndalang mahsuloti bilan aniqlanadi. Natijada, barcha superintegral tizimlar avtomatik ravishda Nambu mexanikasi tomonidan muqobil ravishda va Gamilton mexanikasiga ekvivalent tarzda tavsiflanadi^[31].

Maksimal superintegrallash mumkin bo'lgan tizimlar, quyida ko'rsatilgandek, kommutatsiya munosabatlari yordamida nicellashtirilishi mumkin^[32]. Shunga qaramay, ular ekvivalent tarzda Nambu tizimida kvantlangan, masalan, bu klassik Kepler muammosi kvant vodorod atomiga mos keladi^[33].

Uyg'ongan potensiallar ostida evolyutsiya

Laplas-Runge-Lenz vektor $A$ faqat mukammal teskari kvadrat markaziy kuch uchun saqlanadi. Sayyora harakati kabi ko'pgina amaliy muammolarda esa, ikki jism o'rtasidagi o'zaro ta'sirning potentsial energiyasi mutlaqo teskari kvadrat qonuni emas, balki qo'shimcha markaziy kuchni o'z ichiga olishi mumkin, $h (r)$ potentsial energiya bilan tavsiflangan tebranish . Bunday hollarda LRL vektori orbita tekisligida sekin aylanadi, bu orbitaning sekin apsidal presessiyasiga mos keladi.

Taxminlarga ko'ra, bezovta qiluvchi potentsial $h (r)$ konservativ markaziy kuch bo'lib, u umumiy energiya $E$ va burchak momentum vektori $L$ saqlanishini anglatadi. Shunday qilib, harakat hali ham $L$ ga perpendikulyar tekislikda yotadi va $A 2 = m 2 k 2 + 2 mEL 2$ tenglamadan $A$ kattaligi saqlanib qoladi. Buzilish potentsiali $h (r)$ har qanday funktsiya bo'lishi mumkin, lekin ikkita jism orasidagi asosiy teskari kvadrat kuchdan sezilarli darajada zaif bo'lishi kerak.

LRL vektorining aylanish tezligi bezovta qiluvchi potentsial $h (r)$ haqida ma'lumot beradi. Kanonik tebranish nazariyasi va harakat burchagi koordinatalaridan foydalanib, $A$ tezlik bilan aylanishini ko'rsatish oson^[34].

{\begin{aligned}{\frac {\partial }{\partial L}}\langle h(r)\rangle &={\frac {\partial }{\partial L}}\left\{{\frac {1}{T}}\int _{0}^{T}h(r)\,dt\right\}\\[1em]&={\frac {\partial }{\partial L}}\left\{{\frac {m}{L^{2}}}\int _{0}^{2\pi }r^{2}h(r)\,d\theta \right\},\end{aligned}}

Bu yerda

T

- orbital davri va

L dt = m r 2 dθ

tengligi vaqt integralini burchakli integralga aylantirish uchun ishlatilgan (5-rasm). Burchakli qavs ichidagi ifoda,

Andoza:Langle h (r) Andoza:Rangle

, bezovta qiluvchi potentsialni ifodalaydi, lekin bir to'liq davr uchun o'rtacha hisoblanadi ; ya'ni tananing o'z orbitasini bir marta to'liq o'tishi uchun o'rtacha hisoblanadi. Matematik jihatdan, bu vaqt o'rtacha qiymati jingalak qavslardagi quyidagi miqdorga to'g'ri keladi. Bu o'rtacha aylanish tezligidagi tebranishlarni bostirishga yordam beradi.

Ushbu yondashuv Eynshteynning umumiy nisbiylik nazariyasini tasdiqlash uchun ishlatilgan, bu oddiy Nyuton tortishish potentsialiga kichik samarali teskari kubik tebranish qo'shadi^[35],

h(r)={\frac {kL^{2}}{m^{2}c^{2}}}\left({\frac {1}{r^{3}}}\right).

Bu funksiyani integralga kiritish va tenglamadan foydalanish

{\frac {1}{r}}={\frac {mk}{L^{2}}}\left(1+{\frac {A}{mk}}\cos \theta \right)

r

ni

θ

bilan ifodalash uchun, bu Nyuton bo'lmagan tebranish natijasida kelib chiqqan periapsisning presessiya tezligiga teng deb hisoblanadi^[35].

{\frac {6\pi k^{2}}{TL^{2}c^{2}}},

Bu Merkuriy va ikkilik pulsarlarning kuzatilgan anomal presessiyasiga yaqindan mos keladi^[36]^[37]. Tajriba bilan bu kelishuv umumiy nisbiylik uchun kuchli dalildir^[38] ^[39].

Impuls fazosida vodorod atomi uchun Laplas-Runge-Lenz operatori

Impuls fazosida masshtablangan Laplas-Runge-Lenz operatori yaqinda topilgan^[40] ^[41]. Operator uchun formula pozitsiya fazosiga qaraganda soddaroq:

{\hat {\mathbf {A} }}_{\mathbf {p} }=\imath ({\hat {l}}_{\mathbf {p} }+1)\mathbf {p} -{\frac {(p^{2}+1)}{2}}\imath \mathbf {\nabla } _{\mathbf {p} },

bu yerda "darajali operator"

{\hat {l}}_{\mathbf {p} }=(\mathbf {p} \mathbf {\nabla } _{\mathbf {p} })

bir jinsli ko'phadni darajasiga ko'paytiradi.

Casimir invariantlari va energiya darajalari

Salbiy energiya uchun Casimir invariantlari

{\begin{aligned}C_{1}&=\mathbf {D} \cdot \mathbf {D} +\mathbf {L} \cdot \mathbf {L} ={\frac {mk^{2}}{2|E|}},\\C_{2}&=\mathbf {D} \cdot \mathbf {L} =0,\end{aligned}}

va

D

va

L

ning barcha komponentlari bilan yo'qolib borayotgan Puasson qavslari bor,

\{C_{1},L_{i}\}=\{C_{1},D_{i}\}=\{C_{2},L_{i}\}=\{C_{2},D_{i}\}=0.

C₂ trivial nolga teng, chunki ikkala vektor har doim perpendikulyar.

Biroq, boshqa invariant, C₁, notrivial va faqat $m$ , $k$ va $E$ ga bog'liq. Kanonik kvantlashda bu invariant vodorodga o'xshash atomlarning energiya darajalarini Shredinger tenglamasining an'anaviy yechimi o'rniga faqat kvant mexanik kanonik kommutatsiya munosabatlari yordamida olish imkonini beradi^[8] ^[42]. Ushbu hosila keyingi bobda batafsil muhokama qilinadi.

Kepler masalalarida Laplas-Runge-Lenz vektorining saqlanishini isbotlash

Quyida LRL vektorining teskari kvadrat qonuniga bo'ysunadigan markaziy kuchlar ostida saqlanishini ko'rsatadigan dalillar keltirilgan.

Saqlashning bevosita isboti

Markaziy kuch $\mathbf {F}$ zarrachaga ta'sir qiluvchi

\mathbf {F} ={\frac {d\mathbf {p} }{dt}}=f(r){\frac {\mathbf {r} }{r}}=f(r)\mathbf {\hat {r}}

ba'zi funksiyalar uchun

f(r)

radiusdan

r

. Burchak momenti

\mathbf {L} =\mathbf {r} \times \mathbf {p}

dan beri

{\textstyle {\frac {d}{dt}}\mathbf {L} =0}

markaziy kuchlar ostida saqlanadi, va

{\frac {d}{dt}}\left(\mathbf {p} \times \mathbf {L} \right)={\frac {d\mathbf {p} }{dt}}\times \mathbf {L} =f(r)\mathbf {\hat {r}} \times \left(\mathbf {r} \times m{\frac {d\mathbf {r} }{dt}}\right)=f(r){\frac {m}{r}}\left[\mathbf {r} \left(\mathbf {r} \cdot {\frac {d\mathbf {r} }{dt}}\right)-r^{2}{\frac {d\mathbf {r} }{dt}}\right],

impuls bu yerda

{\textstyle \mathbf {p} =m{\frac {d\mathbf {r} }{dt}}}

va bu yerda uch karra ko'paytma Lagrange formulasi yordamida soddalashtirilgan

\mathbf {r} \times \left(\mathbf {r} \times {\frac {d\mathbf {r} }{dt}}\right)=\mathbf {r} \left(\mathbf {r} \cdot {\frac {d\mathbf {r} }{dt}}\right)-r^{2}{\frac {d\mathbf {r} }{dt}}.

Identifikatsiya

{\frac {d}{dt}}\left(\mathbf {r} \cdot \mathbf {r} \right)=2\mathbf {r} \cdot {\frac {d\mathbf {r} }{dt}}={\frac {d}{dt}}(r^{2})=2r{\frac {dr}{dt}}

tenglamani chiqaradi

{\frac {d}{dt}}\left(\mathbf {p} \times \mathbf {L} \right)=-mf(r)r^{2}\left[{\frac {1}{r}}{\frac {d\mathbf {r} }{dt}}-{\frac {\mathbf {r} }{r^{2}}}{\frac {dr}{dt}}\right]=-mf(r)r^{2}{\frac {d}{dt}}\left({\frac {\mathbf {r} }{r}}\right).

Teskari kvadrat markaziy kuchning maxsus holati uchun

{\textstyle f(r)={\frac {-k}{r^{2}}}}

, bu quyidagiga teng:

{\frac {d}{dt}}\left(\mathbf {p} \times \mathbf {L} \right)=mk{\frac {d}{dt}}\left({\frac {\mathbf {r} }{r}}\right)={\frac {d}{dt}}(mk\mathbf {\hat {r}} ).

Shuning uchun

A

teskari kvadrat markaziy kuchlar uchun saqlanadi ^[43]:

{\frac {d}{dt}}\mathbf {A} ={\frac {d}{dt}}\left(\mathbf {p} \times \mathbf {L} \right)-{\frac {d}{dt}}\left(mk\mathbf {\hat {r}} \right)=\mathbf {0} .

Qisqaroq dalil burchak momentumning burchak tezligiga nisbati yordamida olinadi,

\mathbf {L} =mr^{2}{\boldsymbol {\omega }}

, bu zarrachaga perpendikulyar tekislikda harakatlanadigan zarra uchun amal qiladi

\mathbf {L}

. Teskari-kvadrat markaziy kuchlarni belgilash, vaqt hosilasi

\mathbf {p} \times \mathbf {L}

hisoblanadi

{\frac {d}{dt}}\mathbf {p} \times \mathbf {L} =\left({\frac {-k}{r^{2}}}\mathbf {\hat {r}} \right)\times \left(mr^{2}{\boldsymbol {\omega }}\right)=mk\,{\boldsymbol {\omega }}\times \mathbf {\hat {r}} =mk\,{\frac {d}{dt}}\mathbf {\hat {r}} ,

bu yerda oxirgi tenglik o'rinli bo'ladi, chunki birlik vektor faqat aylanish orqali o'zgarishi mumkin va

{\boldsymbol {\omega }}\times \mathbf {\hat {r}}

aylanuvchi vektorning orbital tezligi. Shunday qilib,

A

teng vaqt hosilalari bo'lgan ikki vektorning ayirmasi sifatida ko'rinadi.

Ushbu maqolaning boshqa qismida tasvirlanganidek, ushbu LRL vektor $A$ umumiy saqlangan vektorning maxsus holatidir ${\mathcal {A}}$ Bu barcha markaziy kuchlar uchun belgilanishi mumkin^[18] ^[19]. Biroq, aksariyat markaziy kuchlar yopiq orbitalarni hosil qilmagani uchun (qarang: Bertran teoremasi ), analog vektor ${\mathcal {A}}$ kamdan-kam hollarda oddiy ta'rifga ega va odatda $r$ va orasidagi $θ$ burchakning ko'p qiymatli funktsiyasidir.

↑ ^1,00 ^1,01 ^1,02 ^1,03 ^1,04 ^1,05 ^1,06 ^1,07 ^1,08 ^1,09 ^1,10 ^1,11 Goldstein, H.. Classical Mechanics, 2nd, Addison Wesley, 1980 — 102–105, 421–422 bet. Manba xatosi: Invalid <ref> tag; name "goldstein_1980" defined multiple times with different content
↑ ^2,0 ^2,1 ^2,2 Taff, L. G.. Celestial Mechanics: A Computational Guide for the Practitioner. New York: John Wiley and Sons, 1985 — 42–43 bet.
↑ Goldstein, H.. Classical Mechanics, 2nd, Addison Wesley, 1980 — 94–102 bet.
↑ Arnold, V. I.. Mathematical Methods of Classical Mechanics, 2nd, New York: Springer-Verlag, 1989 — 38 bet. ISBN 0-387-96890-3.
↑ Sommerfeld, A.. Mechanics, 4th, Lectures on Theoretical Physics, New York: Academic Press, 1964 — 38–45 bet.
↑ Lanczos, C.. The Variational Principles of Mechanics, 4th, New York: Dover Publications, 1970 — 118, 129, 242, 248 bet.
↑ ^7,0 ^7,1 Pauli, W. (1926). "Über das Wasserstoffspektrum vom Standpunkt der neuen Quantenmechanik". Zeitschrift für Physik 36 (5): 336–363. doi:10.1007/BF01450175.
↑ ^8,0 ^8,1 ^8,2 Bohm, A.. Quantum Mechanics: Foundations and Applications, 3rd, New York: Springer-Verlag, 1993 — 205–222 bet.
↑ Hanca, J.; Tulejab, S.; Hancova, M. (2004). "Symmetries and conservation laws: Consequences of Noether's theorem". American Journal of Physics 72 (4): 428–35. doi:10.1119/1.1591764. http://www.eftaylor.com/pub/symmetry.html.
↑ Fock, V. (1935). "Zur Theorie des Wasserstoffatoms". Zeitschrift für Physik 98 (3–4): 145–154. doi:10.1007/BF01336904.
↑ Bargmann, V. (1936). "Zur Theorie des Wasserstoffatoms: Bemerkungen zur gleichnamigen Arbeit von V. Fock". Zeitschrift für Physik 99 (7–8): 576–582. doi:10.1007/BF01338811.
↑ ^12,0 ^12,1 Hamilton, W. R. (1847). "The hodograph or a new method of expressing in symbolic language the Newtonian law of attraction". Proceedings of the Royal Irish Academy 3: 344–353.
↑ Goldstein, H.. Classical Mechanics, 2nd, Addison Wesley, 1980 — 421 bet.
↑ ^14,0 ^14,1 ^14,2 ^14,3 Arnold, V. I.. Mathematical Methods of Classical Mechanics, 2nd, New York: Springer-Verlag, 1989 — 413–415 bet. ISBN 0-387-96890-3.
↑ ^15,0 ^15,1 ^15,2 ^15,3 ^15,4 ^15,5 Goldstein, H. (1975). "Prehistory of the Runge–Lenz vector". American Journal of Physics 43 (8): 737–738. doi:10.1119/1.9745.

Goldstein, H. (1976). "More on the prehistory of the Runge–Lenz vector". American Journal of Physics 44 (11): 1123–1124. doi:10.1119/1.10202. Manba xatosi: Invalid <ref> tag; name "goldstein_1975_1976" defined multiple times with different content
↑ ^16,0 ^16,1 ^16,2 Hamilton, W. R. (1847). "Applications of Quaternions to Some Dynamical Questions". Proceedings of the Royal Irish Academy 3: Appendix III.
↑ ^17,0 ^17,1 Landau, L. D.. Mechanics, 3rd, Pergamon Press, 1976 — 154 bet. ISBN 0-08-021022-8. Manba xatosi: Invalid <ref> tag; name "landau_lifshitz_1976" defined multiple times with different content
↑ ^18,0 ^18,1 ^18,2 Fradkin, D. M. (1967). "Existence of the Dynamic Symmetries O₄ and SU₃ for All Classical Central Potential Problems". Progress of Theoretical Physics 37 (5): 798–812. doi:10.1143/PTP.37.798.
↑ ^19,0 ^19,1 ^19,2 Yoshida, T. (1987). "Two methods of generalisation of the Laplace–Runge–Lenz vector". European Journal of Physics 8 (4): 258–259. doi:10.1088/0143-0807/8/4/005.
↑ ^20,0 ^20,1 Goldstein, H.. Classical Mechanics, 2nd, Addison Wesley, 1980 — 1–11 bet.
↑ ^21,0 ^21,1 Symon, K. R.. Mechanics, 3rd, Addison Wesley, 1971 — 103–109, 115–128 bet.
↑ Hermann, J. (1710). "Metodo d'investigare l'Orbite de' Pianeti, nell' ipotesi che le forze centrali o pure le gravità degli stessi Pianeti sono in ragione reciproca de' quadrati delle distanze, che i medesimi tengono dal Centro, a cui si dirigono le forze stesse". Giornale de Letterati d'Italia 2: 447–467.

Hermann, J. (1710). "Extrait d'une lettre de M. Herman à M. Bernoulli datée de Padoüe le 12. Juillet 1710". Histoire de l'Académie Royale des Sciences 1732: 519–521.
↑ Bernoulli, J. (1710). "Extrait de la Réponse de M. Bernoulli à M. Herman datée de Basle le 7. Octobre 1710". Histoire de l'Académie Royale des Sciences 1732: 521–544.
↑ Laplace, P. S.. Traité de mécanique celeste. Paris, Duprat, 1799 — Tome I, Premiere Partie, Livre II, pp.165ff bet.
↑ Gibbs, J. W.. Vector Analysis. New York: Scribners, 1901 — 135 bet.
↑ Runge, C.. Vektoranalysis. Leipzig: Hirzel, 1919.
↑ Lenz, W. (1924). "Über den Bewegungsverlauf und Quantenzustände der gestörten Keplerbewegung". Zeitschrift für Physik 24 (1): 197–207. doi:10.1007/BF01327245.
↑ Symon, K. R.. Mechanics, 3rd, Addison Wesley, 1971 — 130–131 bet.
↑ Evans, N. W. (1990). "Superintegrability in classical mechanics". Physical Review A 41 (10): 5666–5676. doi:10.1103/PhysRevA.41.5666. PMID 9902953.
↑ Sommerfeld, A.. Atomic Structure and Spectral Lines. London: Methuen, 1923 — 118 bet.
↑ Curtright, T.; Zachos C. (2003). "Classical and Quantum Nambu Mechanics". Physical Review D68 (8): 085001. doi:10.1103/PhysRevD.68.085001.
↑ Evans, N. W. (1991). "Group theory of the Smorodinsky–Winternitz system". Journal of Mathematical Physics 32 (12): 3369–3375. doi:10.1063/1.529449.
↑ Zachos, C.; Curtright T. (2004). "Branes, quantum Nambu brackets, and the hydrogen atom". Czech Journal of Physics 54 (11): 1393–1398. doi:10.1007/s10582-004-9807-x.
↑ Goldstein, H.. Classical Mechanics, 2nd, Addison Wesley, 1980 — 102–105, 421–422 bet.
↑ ^35,0 ^35,1 Einstein, A. (1915). "Erklärung der Perihelbewegung des Merkur aus der allgemeinen Relativitätstheorie". Sitzungsberichte der Preussischen Akademie der Wissenschaften 1915: 831–839.
↑ Le Verrier, U. J. J. (1859). "Lettre de M. Le Verrier à M. Faye sur la Théorie de Mercure et sur le Mouvement du Périhélie de cette Planète". Comptes Rendus de l'Académie des Sciences de Paris 49: 379–383.
↑ Will, C. M.. General Relativity, an Einstein Century Survey, SW Hawking and W Israel, Cambridge: Cambridge University Press, 1979 — Chapter 2 bet.
↑ Pais, A.. Subtle is the Lord: The Science and the Life of Albert Einstein. Oxford University Press, 1982.
↑ Roseveare, N. T.. Mercury's Perihelion from Le Verrier to Einstein. Oxford University Press, 1982. ISBN 978-0-19-858174-1.
↑ Efimov, S.P. (2022). "Coordinate space modification of Fock's theory. Harmonic tensors in the quantum Coulomb problem". Physics-Uspekhi 65 (9): 952–967. doi:10.3367/UFNe.2021.04.038966.
↑ Efimov, S.P. (2023). "Runge-Lenz Operator in the Momentum Space". JETP Letters 117 (9): 716–720. doi:10.1134/S0021364023600635.
↑ Hall 2013
↑ Hall 2013 Proposition 2.34.

[goldstein_1980-1] 1,00 ^1,01 ^1,02 ^1,03 ^1,04 ^1,05 ^1,06 ^1,07 ^1,08 ^1,09 ^1,10 ^1,11 Goldstein, H.. Classical Mechanics, 2nd, Addison Wesley, 1980 — 102–105, 421–422 bet. Manba xatosi: Invalid <ref> tag; name "goldstein_1980" defined multiple times with different content

[taff_1985-2] 2,0 ^2,1 ^2,2 Taff, L. G.. Celestial Mechanics: A Computational Guide for the Practitioner. New York: John Wiley and Sons, 1985 — 42–43 bet.

[goldstein_1980b-3] Goldstein, H.. Classical Mechanics, 2nd, Addison Wesley, 1980 — 94–102 bet.

[arnold_1989-4] Arnold, V. I.. Mathematical Methods of Classical Mechanics, 2nd, New York: Springer-Verlag, 1989 — 38 bet. ISBN 0-387-96890-3.

[sommerfeld_1989-5] Sommerfeld, A.. Mechanics, 4th, Lectures on Theoretical Physics, New York: Academic Press, 1964 — 38–45 bet.

[lanczos_1970-6] Lanczos, C.. The Variational Principles of Mechanics, 4th, New York: Dover Publications, 1970 — 118, 129, 242, 248 bet.

[pauli_1926-7] 7,0 ^7,1 Pauli, W. (1926). "Über das Wasserstoffspektrum vom Standpunkt der neuen Quantenmechanik". Zeitschrift für Physik 36 (5): 336–363. doi:10.1007/BF01450175.

[bohm_1993-8] 8,0 ^8,1 ^8,2 Bohm, A.. Quantum Mechanics: Foundations and Applications, 3rd, New York: Springer-Verlag, 1993 — 205–222 bet.

[hanca_et_al_2004-9] Hanca, J.; Tulejab, S.; Hancova, M. (2004). "Symmetries and conservation laws: Consequences of Noether's theorem". American Journal of Physics 72 (4): 428–35. doi:10.1119/1.1591764. http://www.eftaylor.com/pub/symmetry.html.

[fock_1935-10] Fock, V. (1935). "Zur Theorie des Wasserstoffatoms". Zeitschrift für Physik 98 (3–4): 145–154. doi:10.1007/BF01336904.

[bargmann_1936-11] Bargmann, V. (1936). "Zur Theorie des Wasserstoffatoms: Bemerkungen zur gleichnamigen Arbeit von V. Fock". Zeitschrift für Physik 99 (7–8): 576–582. doi:10.1007/BF01338811.

[hamilton_1847_hodograph-12] 12,0 ^12,1 Hamilton, W. R. (1847). "The hodograph or a new method of expressing in symbolic language the Newtonian law of attraction". Proceedings of the Royal Irish Academy 3: 344–353.

[goldstein_1980c-13] Goldstein, H.. Classical Mechanics, 2nd, Addison Wesley, 1980 — 421 bet.

[arnold_1989b-14] 14,0 ^14,1 ^14,2 ^14,3 Arnold, V. I.. Mathematical Methods of Classical Mechanics, 2nd, New York: Springer-Verlag, 1989 — 413–415 bet. ISBN 0-387-96890-3.

[goldstein_1975_1976-15] 15,0 ^15,1 ^15,2 ^15,3 ^15,4 ^15,5 Goldstein, H. (1975). "Prehistory of the Runge–Lenz vector". American Journal of Physics 43 (8): 737–738. doi:10.1119/1.9745.

Goldstein, H. (1976). "More on the prehistory of the Runge–Lenz vector". American Journal of Physics 44 (11): 1123–1124. doi:10.1119/1.10202. Manba xatosi: Invalid <ref> tag; name "goldstein_1975_1976" defined multiple times with different content

[hamilton_1847_quaternions-16] 16,0 ^16,1 ^16,2 Hamilton, W. R. (1847). "Applications of Quaternions to Some Dynamical Questions". Proceedings of the Royal Irish Academy 3: Appendix III.

[landau_lifshitz_1976-17] 17,0 ^17,1 Landau, L. D.. Mechanics, 3rd, Pergamon Press, 1976 — 154 bet. ISBN 0-08-021022-8. Manba xatosi: Invalid <ref> tag; name "landau_lifshitz_1976" defined multiple times with different content

[fradkin_1967-18] 18,0 ^18,1 ^18,2 Fradkin, D. M. (1967). "Existence of the Dynamic Symmetries O₄ and SU₃ for All Classical Central Potential Problems". Progress of Theoretical Physics 37 (5): 798–812. doi:10.1143/PTP.37.798.

[yoshida_1987-19] 19,0 ^19,1 ^19,2 Yoshida, T. (1987). "Two methods of generalisation of the Laplace–Runge–Lenz vector". European Journal of Physics 8 (4): 258–259. doi:10.1088/0143-0807/8/4/005.

[goldstein_1980d-20] 20,0 ^20,1 Goldstein, H.. Classical Mechanics, 2nd, Addison Wesley, 1980 — 1–11 bet.

[symon_1971-21] 21,0 ^21,1 Symon, K. R.. Mechanics, 3rd, Addison Wesley, 1971 — 103–109, 115–128 bet.

[22] Hermann, J. (1710). "Metodo d'investigare l'Orbite de' Pianeti, nell' ipotesi che le forze centrali o pure le gravità degli stessi Pianeti sono in ragione reciproca de' quadrati delle distanze, che i medesimi tengono dal Centro, a cui si dirigono le forze stesse". Giornale de Letterati d'Italia 2: 447–467.

Hermann, J. (1710). "Extrait d'une lettre de M. Herman à M. Bernoulli datée de Padoüe le 12. Juillet 1710". Histoire de l'Académie Royale des Sciences 1732: 519–521.

[23] Bernoulli, J. (1710). "Extrait de la Réponse de M. Bernoulli à M. Herman datée de Basle le 7. Octobre 1710". Histoire de l'Académie Royale des Sciences 1732: 521–544.

[24] Laplace, P. S.. Traité de mécanique celeste. Paris, Duprat, 1799 — Tome I, Premiere Partie, Livre II, pp.165ff bet.

[25] Gibbs, J. W.. Vector Analysis. New York: Scribners, 1901 — 135 bet.

[26] Runge, C.. Vektoranalysis. Leipzig: Hirzel, 1919.

[27] Lenz, W. (1924). "Über den Bewegungsverlauf und Quantenzustände der gestörten Keplerbewegung". Zeitschrift für Physik 24 (1): 197–207. doi:10.1007/BF01327245.

[symon_1971b-28] Symon, K. R.. Mechanics, 3rd, Addison Wesley, 1971 — 130–131 bet.

[29] Evans, N. W. (1990). "Superintegrability in classical mechanics". Physical Review A 41 (10): 5666–5676. doi:10.1103/PhysRevA.41.5666. PMID 9902953.

[30] Sommerfeld, A.. Atomic Structure and Spectral Lines. London: Methuen, 1923 — 118 bet.

[31] Curtright, T.; Zachos C. (2003). "Classical and Quantum Nambu Mechanics". Physical Review D68 (8): 085001. doi:10.1103/PhysRevD.68.085001.

[32] Evans, N. W. (1991). "Group theory of the Smorodinsky–Winternitz system". Journal of Mathematical Physics 32 (12): 3369–3375. doi:10.1063/1.529449.

[33] Zachos, C.; Curtright T. (2004). "Branes, quantum Nambu brackets, and the hydrogen atom". Czech Journal of Physics 54 (11): 1393–1398. doi:10.1007/s10582-004-9807-x.

[goldstein_19802-34] Goldstein, H.. Classical Mechanics, 2nd, Addison Wesley, 1980 — 102–105, 421–422 bet.

[einstein_1915-35] 35,0 ^35,1 Einstein, A. (1915). "Erklärung der Perihelbewegung des Merkur aus der allgemeinen Relativitätstheorie". Sitzungsberichte der Preussischen Akademie der Wissenschaften 1915: 831–839.

[36] Le Verrier, U. J. J. (1859). "Lettre de M. Le Verrier à M. Faye sur la Théorie de Mercure et sur le Mouvement du Périhélie de cette Planète". Comptes Rendus de l'Académie des Sciences de Paris 49: 379–383.

[37] Will, C. M.. General Relativity, an Einstein Century Survey, SW Hawking and W Israel, Cambridge: Cambridge University Press, 1979 — Chapter 2 bet.

[38] Pais, A.. Subtle is the Lord: The Science and the Life of Albert Einstein. Oxford University Press, 1982.

[39] Roseveare, N. T.. Mercury's Perihelion from Le Verrier to Einstein. Oxford University Press, 1982. ISBN 978-0-19-858174-1.

[40] Efimov, S.P. (2022). "Coordinate space modification of Fock's theory. Harmonic tensors in the quantum Coulomb problem". Physics-Uspekhi 65 (9): 952–967. doi:10.3367/UFNe.2021.04.038966.

[41] Efimov, S.P. (2023). "Runge-Lenz Operator in the Momentum Space". JETP Letters 117 (9): 716–720. doi:10.1134/S0021364023600635.

[ReferenceA-42] Hall 2013

[43] Hall 2013 Proposition 2.34.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]