Lorens almashtirish formulalari

 

Maksvell tenglamalaridan tortib, Eynshteynning maxsus nisbiylik postulatlari va elementar algebra va giperbolik funksiyalardan tortib chiziqli algebra va guruhlar nazariyasiga qadar boʻlgan matematik vositalardan tortib, turli fizik prinsiplardan foydalangan holda Lorentz oʻzgarishlarini olishning koʻplab usullari mavjud.

Ushbu maqola maxsus nisbiylik kontekstida kuzatish uchun qulay boʻlgan bir nechtasini taqdim etadi, standart konfiguratsiyadagi Lorentz kuchayishining eng oddiy holati uchun, yaʼni tezlikdan kamroq doimiy (bir xil) nisbiy tezlikda bir-biriga nisbatan harakatlanadigan ikkita inertial ramka yorugʻlik va x va x ′ oʻqlari kollinear boʻlishi uchun Kartezyen koordinatalaridan foydalangan holda.

Zamonaviy fizikaning asosiy sohalarida, yaʼni umumiy nisbiylik va uning keng qoʻllaniladigan maxsus nisbiylik toʻplamida, shuningdek relativistik kvant mexanikasi va relativistik kvant maydon nazariyasida Lorentz transformatsiyasi transformatsiya qoidasi boʻlib, unga koʻra barcha toʻrt vektor va fizik miqdorlarni oʻz ichiga olgan tensorlar oʻzgaradi. bir mos yozuvlar ramkasidan boshqasiga.

Bunday toʻrt vektorning asosiy misollari zarrachaning toʻrt pozitsiyasi va toʻrt momentumi, maydonlar uchun esa elektromagnit tensor va kuchlanish-energiya tensoridir. Bu ob'ektlarning Lorentz oʻzgarishiga koʻra oʻzgarishi ularni vektorlar va tenzorlar sifatida matematik tarzda belgilaydi.

Baʼzi bir ramkadagi toʻrt vektor yoki tensorlarning tarkibiy qismlarini hisobga olgan holda, "transformatsiya qoidasi" bir xil toʻrt vektor yoki tensorlarning boshqa ramkadagi oʻzgartirilgan komponentlarini aniqlashga imkon beradi, ular kuchaytirilishi yoki tezlashtirilishi mumkin, dastlabki ramkaga nisbatan. "Boost" ni fazoviy tarjima bilan aralashtirib yubormaslik kerak, aksincha u kadrlar orasidagi nisbiy tezlik bilan tavsiflanadi. Transformatsiya qoidasining oʻzi ramkalarning nisbiy harakatiga bogʻliq. Ikki inertial ramkaning eng oddiy holatida ular orasidagi nisbiy tezlik transformatsiya qoidasiga kiradi. Aylanadigan mos yozuvlar ramkalari yoki umumiy inertial boʻlmagan mos yozuvlar tizimlari uchun nisbiy tezlik (kattalik va yoʻnalish), aylanish oʻqi va burchakni oʻz ichiga olgan koʻproq parametrlar kerak boʻladi.

Tarixiy nazar

Odatiy tuzatma (masalan, Albert Eynshteynning asl ishi) yorugʻlik tezligining oʻzgarmasligiga asoslanadi. Biroq, bu har doim ham boshlangʻich nuqta emas: haqiqatan ham (masalan, Landau va Lifshitsning nazariy fizika kursining ikkinchi jildida tasvirlanganidek), haqiqatda oʻzaro taʼsirlarning joylashuvi xavf ostida: bir zarraning, aytaylik, boshqasiga taʼsir qiladigan taʼsiri, bir zumda uzatilishi mumkin emas. Demak, axborot uzatishning nazariy maksimal tezligi mavjud boʻlib, u oʻzgarmas boʻlishi kerak va bu tezlik vakuumdagi yorugʻlik tezligiga toʻgʻri keladi. Nyutonning oʻzi uzoqdan harakat qilish gʻoyasini falsafiy jihatdan "absurd" deb atagan va tortishish maʼlum qonunlarga koʻra qandaydir vosita tomonidan uzatilishi kerak deb hisoblagan.

1964-yilgi maqolada Erik Kristofer Zeeman koordinata oʻzgarishlari Lorents oʻzgarishlari ekanligini taʼminlash uchun matematik maʼnoda yorugʻlik tezligining oʻzgarmasligidan koʻra zaifroq boʻlgan sabab -oqibatni saqlovchi xususiyat etarli ekanligini koʻrsatdi. Norman Goldshteynning qogʻozi shunga oʻxshash natijani sabablik emas, balki inertiallik (vaqtga oʻxshash chiziqlarning saqlanishi) yordamida koʻrsatadi.

Fizik prinsiplar

Eynshteyn maxsus nisbiylik nazariyasini ikkita asosiy postulatga asoslagan edi. Birinchidan, barcha fizik qonunlar nisbiy harakat holatidan qat’iy nazar barcha inertsial sanoq sistemalari uchun bir xil. Ikkinchidan, yorugʻlikning boʻsh fazodagi tezligi barcha inertial sanoq sistemalarida bir xil boʻladi, yana har bir sanoq sistemasining nisbiy tezligidan qatʼiy nazar. Lorents konvertatsiyasi asosan ushbu ikkinchi postulatning bevosita natijasidir.

Ikkinchi postulat

Yorugʻlik tezligining mos yozuvlar tizimiga bogʻliq boʻlmagan doimiyligini koʻrsatadigan maxsus nisbiylikning ikkinchi postulatini qabul qiling va bir-biriga nisbatan doimiy tezlik bilan harakatlanadigan, yaʼni inertial tizimlar toʻplamini koʻrib chiqing, ularning har biri oʻz Dekart toʻplamiga ega. nuqtalarni, yaʼni fazo-vaqt hodisalarini belgilovchi koordinatalar . Yorugʻlik tezligining oʻzgarmasligini matematik shaklda ifodalash uchun fazo-vaqtdagi ikkita hodisani aniqlang, ular har bir mos yozuvlar tizimida qayd etiladi. Birinchi hodisa yorugʻlik signalining emissiyasi, ikkinchisi esa uning soʻrilishi boʻlsin.

Toʻplamdagi har qanday mos yozuvlar ramkasini tanlang. Uning koordinatalarida birinchi hodisaga koordinatalar tayinlanadi $x_{1},y_{1},z_{1},ct_{1}$ va ikkinchisi $x_{2},y_{2},z_{2},ct_{2}$ . Emissiya va yutilish orasidagi fazoviy masofa ${\textstyle {\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}+(z_{2}-z_{1})^{2}}}}$, lekin bu ham masofa $c(t_{2}-t_{1})$ signal orqali harakatlanadi. Shunday qilib, tenglamani oʻrnatish mumkin

$c^{2}(t_{2}-t_{1})^{2}-(x_{2}-x_{1})^{2}-(y_{2}-y_{1})^{2}-(z_{2}-z_{1})^{2}=0.$

Har bir boshqa koordinata tizimi oʻz koordinatalarida bir xil tenglamani yozib oladi. Bu yorugʻlik tezligining oʻzgarmasligining bevosita matematik natijasidir. Chapdagi miqdor fazoviy vaqt oraligʻi deb ataladi. Interval yorugʻlik signallari bilan ajratilgan hodisalar uchun barcha mos yozuvlar ramkalarida bir xil (nol) boʻladi va shuning uchun oʻzgarmas deb ataladi.

Intervalning oʻzgarmasligi

Lorentz oʻzgarishi tabiat tomonidan amalga oshirilgan jismoniy ahamiyatga ega boʻlishi uchun interval faqat yorugʻlik signallari bilan ajratilgan hodisalar uchun emas, balki har qanday ikkita hodisa uchun oʻzgarmas oʻlchov boʻlishi juda muhimdir. Buni aniqlash uchun cheksiz kichik oraliq hisobga olinadi, $ds^{2}=c^{2}dt^{2}-dx^{2}-dy^{2}-dz^{2},$ tizimda qayd etilganidek $K$ . Mayli $K'$ intervalni tayinlaydigan boshqa tizim boʻlsin $ds'^{2}$ bir xil ikki cheksiz ajratilgan hodisaga. Chunki agar $ds^{2}=0$, keyin interval boshqa har qanday tizimda ham nolga teng boʻladi (ikkinchi postulat) va beri $ds^{2}$ va $ds'^{2}$ bir xil tartibdagi cheksiz kichiklar, ular bir-biriga proportsional boʻlishi kerak,

$ds^{2}=ads'^{2}.$

Nima boʻlishi mumkin $a$ bogʻliqmi? Bu ikki hodisaning fazo-vaqtdagi pozitsiyalariga bogʻliq boʻlmasligi mumkin, chunki bu fazoviy vaqtning postulatsiyalangan bir xilligini buzadi. Bu nisbiy tezlikka bogʻliq boʻlishi mumkin $V'$ orasida $K$ va $K'$, lekin faqat tezlik boʻyicha, yoʻnalish boʻyicha emas, chunki ikkinchisi kosmosning izotropiyasini buzadi.

Endi tizimlarni kiriting $K_{1}$ va $K_{2}$,

$ds^{2}=a(V_{1})ds_{1}^{2},\quad ds^{2}=a(V_{2})ds_{2}^{2},\quad ds_{1}^{2}=a(V_{12})ds_{2}^{2}.$

Bulardan kelib chiqadiki,

${\frac {a(V_{2})}{a(V_{1})}}=a(V_{12}).$

Endi oʻng tomonda buni kuzatish mumkin $V_{12}$ ikkalasiga bogʻliq $V_{1}$ va $V_{2}$; shuningdek vektorlar orasidagi burchakda ${\textbf {V}}_{1}$ va ${\textbf {V}}_{2}$ . Biroq, chap tomonning bu burchakka bogʻliq emasligi ham kuzatiladi. Shunday qilib, tenglama toʻgʻri boʻlishining yagona yoʻli bu funksiyadir $a(V)$ doimiy hisoblanadi. Bundan tashqari, xuddi shu tenglama boʻyicha bu doimiy birlikdir. Shunday qilib,

$ds^{2}=ds'^{2}$

barcha tizimlar uchun $K'$. Bu barcha cheksiz kichik intervallar uchun amal qilganligi sababli, u barcha intervallar uchun amal qiladi.

Lorentz oʻzgarishlarining barcha boʻlmasa ham, koʻpchilik hosilalari buni odatiy hol sifatida qabul qiladi. Ushbu hosilalarda ular faqat yorugʻlik tezligining doimiyligidan (nurga oʻxshash ajratilgan hodisalarning oʻzgarmasligi) foydalanadilar. Bu natija Lorents transformatsiyasining toʻgʻri transformatsiya ekanligini taʼminlaydi.

Qattiq bayonot va ds² va ds′² mutanosibligini isbotlash

Izohlar.

• Yuqoridagi boʻlimda "cheksiz kichik" atamasi bilan bogʻliq $ds^{2}$ aslida toʻrt oʻlchovli haqiqiy vektor fazosi (yaʼni fazo-vaqt manifoldining nuqtasidagi tangens fazo) ustidagi kvadratik shaklga (nuqta yoʻnalishi boʻyicha) ishora qiladi. Yuqoridagi argument Landau va Lifshitsdan deyarli soʻzma-soʻz koʻchirilgan, bu yerda proportsionallik $ds^{2}$ va $ds'^{2}$ Bu gap matematik jihatdan aniq shakllantirilmagan va isbotlanmagan boʻlsa ham, shunchaki "ravshan" fakt sifatida ifodalanadi. Bu oqlanishi kerak boʻlgan aniq boʻlmagan matematik fakt; Yaxshiyamki, dalil nisbatan sodda va u asosiy algebraik kuzatishlar va manipulyatsiyalarni tashkil qiladi.
• Yuqoridagi taxminlar $h$ quyidagilarni anglatadi: $h:V\times V\to \mathbb {R}$ simmetrik va degenerativ boʻlmagan ikki chiziqli shakl boʻlib, tartibli asos mavjud. $\{v_{1},\dots ,v_{n},v_{n+1},\dots ,v_{d}\}$ ning $V$ buning uchun
  $$h(v_{a},v_{b})={\begin{cases}-1&{\text{if }}a=b\in \{1,\dots ,n\}\\1&{\text{if }}a=b\in \{n+1,\dots ,d\}\\0&{\text{ otherwise}}\end{cases}}$$
• bu yerda maxsus holatni koʻrib chiqsak $n=1,p=3$ keyin biz nisbiylik asosi boʻlgan 4 oʻlchovli Lorentsian imzosining holati bilan shugʻullanamiz (yoki umumiy minus belgisi bilan qarama-qarshi konventsiyani qabul qilish mumkin; lekin bu teoremaning haqiqatiga taʼsir qilmaydi). Bundan tashqari, bu holatda, agar biz taxmin qilsak $g$ va $h$ ikkalasi ham bir xil null toʻplamga ega kvadratik shakllarga ega (fizika terminologiyasida biz buni aytamiz $g$ va $h$ bir xil yorugʻlik konusini keltirib chiqaradi) u holda teorema bizga doimiy borligini aytadi $C>0$ shu kabi $g=Ch$ . Belgilanishdagi baʼzi farqlarni modullash, yuqoridagi boʻlimda aynan shu narsa ishlatilgan.

Teoremani isbotlash.

Asosni tuzatish $\{v_{1},\dots ,v_{d}\}$ ning $V$ qaysiga nisbatan $h$ matritsali tasvirga ega $[h]={\begin{pmatrix}-I_{n}&0\\0&I_{p}\end{pmatrix}}$ . Gap shundaki, vektor fazosi $V$ pastki fazolarga parchalanishi mumkin $V^{-}$ (birinchisining oraligʻi $n$ bazis vektorlari) va $V^{+}$ (keyin ikkinchisining oraligʻi $p$ bazis vektorlari) shundayki, har bir vektor ichida $V$ kabi noyob tarzda yozilishi mumkin $v+w$ uchun $v\in V^{-}$ va $w\in V^{+}$ ; bundan tashqari $h(v,v)\leq 0$, $h(w,w)\geq 0$ va $h(v,w)=0$ . Shunday qilib (binolik boʻyicha)

$h(v+w,v+w)=h(v,v)+h(w,w)$

Oʻngdagi birinchi yigʻindi ijobiy boʻlmaganda, ikkinchisi esa salbiy boʻlmaganda, har qanday uchun $v\in V^{-}$ va $w\in V^{+}$, biz skalyarni topishimiz mumkin $\alpha$ shu kabi $h(v+\alpha w,v+\alpha w)=0$ .

Bundan buyon har doim oʻylab koʻring $v\in V^{-}$ va $w\in V^{+}$ . Ikkilik bilan

${\begin{aligned}g(v+w,v+w)&=g(v,v)+g(w,w)+2g(v,w)\\g(v-w,v-w)&=g(v,v)+g(w,w)-2g(v,w)\end{aligned}}$

Agar $h(v+w,v+w)=0$, keyin ham $h(v-w,v-w)=0$ uchun ham xuddi shunday $g$ (nol toʻplamidan beri $h$ tarkibida mavjud $g$). Bunday holda, yuqoridagi ikkita ifodani ayirish (va 4 ga boʻlish) hosil boʻladi

$0=g(v,w)$

Yuqoridagi kabi, har biri uchun $v\in V^{-}$ va $w\in V^{+}$, skalyar mavjud $\alpha$ shu kabi $h(v+\alpha w,v+\alpha w)=0$, shunday $g(v,\alpha w)=0$, bu ikki chiziqlilikni anglatadi $g(v,w)=0$.

Endi nolga teng boʻlmaganini koʻrib chiqing $v,v'\in V^{-}$ shu kabi $h(v,v)=h(v',v')$ . Biz topamiz $w\in V^{+}$ shu kabi $0=h(v+w,v+w)=h(v,v)+h(w,w)=h(v'+w,v'+w)$ . Yuqoridagi iboralarga koʻra,

$g(v,v)=-g(w,w)=g(v',v')$

Analog tarzda, uchun $w,w'\in V^{+}$, agar buni koʻrsatish mumkin $h(w,w)=h(w',w')$, keyin ham $g(w,w)=g(w',w')$ . Shunday qilib, u barcha vektorlar uchun amal qiladi $V$.

Uchun $u,u'\in V$, agar $g(u,u)=Ch(u,u)\neq 0$, $g(u',u')=C'h(u',u')\neq 0$ baʼzilar uchun $C,C'\in \mathbb {R}$, biz (agar kerak boʻlsa, ulardan birini masshtablash) taxmin qilishimiz mumkin $h(u,u)=h(u',u')$, bu yuqoridagi maʼnoni anglatadi $C=C'$ . Shunday qilib $g=Ch$.

Nihoyat, agar biz buni taxmin qilsak $g,h$ ikkalasi ham imzo turlariga ega $(n,p)$ va $n\neq p$ keyin $C>0$ (bizda mumkin emas $C=0$ chunki bu degani $g=0$ Imzo turiga ega boʻlgani uchun bu mumkin emas $(n,p)$ nolga teng boʻlmagan ikki chiziqli shakl ekanligini bildiradi. Bundan tashqari, agar $C<0$, keyin bu degani $g$ ega $n$ ijobiy diagonal yozuvlar va $p$ salbiy diagonal yozuvlar; yaʼni imzosi bor $(p,n)\neq (n,p)$, biz taxmin qilganimizdan beri $n\neq p$, shuning uchun bu ham mumkin emas. Bu bizni qoldiradi $C>0$ yagona variant sifatida). Bu teoremani isbotlashni tugatadi.

Standart konfiguratsiya

Har bir kuzatuvchi tomonidan inertial mos yozuvlar tizimida (standart konfiguratsiyada) o'lchanadigan hodisaning fazo-vaqt koordinatalari nutq pufakchalarida ko'rsatilgan.
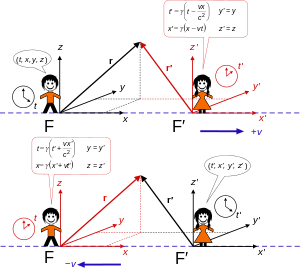
Yuqori: F ′ ramka F ramkaning x o'qi bo'ylab v tezlikda harakat qiladi.
Pastki: F ramka F ′ ramkasining x ′-o'qi bo'ylab − v tezlikda harakat qiladi.

Invariant intervalni fazoda musbat boʻlmagan aniq masofa funksiyasi sifatida koʻrish mumkin. Qidirilayotgan oʻzgarishlar toʻplami bu masofani oʻzgarmas qoldirishi kerak. Malumot tizimi koordinata tizimining kartezian xususiyatidan kelib chiqqan holda, Evklid misolida boʻlgani kabi, mumkin boʻlgan oʻzgarishlar tarjimalar va aylanishlardan iborat, degan xulosaga keladi, bu yerda aylanish atamasi uchun biroz kengroq maʼnoga ruxsat berilishi kerak.Interval tarjima ostida juda oʻzgarmasdir. Aylanish uchun toʻrtta koordinata mavjud. Demak, oltita aylanish tekisligi mavjud. Ulardan uchtasi fazoviy tekisliklarda aylanishdir. Oddiy aylanishlarda ham interval oʻzgarmasdir.

Qolgan uchta koordinata tekisligida intervalni oʻzgarmas qoldiradigan "aylanish" ni topish qoladi. Shu bilan birga, harakatlanuvchi ramkaga mos keladigan koordinatalar bilan mos keladigan koordinatalarni belgilash yoʻlini topish.

Umumiy muammo shunday transformatsiyani topishdir

${\begin{aligned}&c^{2}(t_{2}-t_{1})^{2}-(x_{2}-x_{1})^{2}-(y_{2}-y_{1})^{2}-(z_{2}-z_{1})^{2}\\={}&c^{2}(t_{2}'-t_{1}')^{2}-(x_{2}'-x_{1}')^{2}-(y_{2}'-y_{1}')^{2}-(z_{2}'-z_{1}')^{2}.\end{aligned}}$

Umumiy muammoni hal qilish uchun tarjimalar va oddiy aylanishlar oraligʻining oʻzgarmasligi haqidagi bilimlardan foydalanib, umumiylikni yoʻqotmasdan, F va F′ ramkalar ularning koordinata oʻqlari hammasi boʻladigan tarzda tekislangan deb taxmin qilish mumkin. t = t′ = 0 da uchrashadi va x va x′ oʻqlari doimiy ravishda tekislanadi va F′ tizimi musbat x-axis boʻylab V tezlikka ega. Buni standart konfiguratsiya deb nomlang. Bu shunday transformatsiyani topish uchun umumiy muammoni kamaytiradi

$c^{2}(t_{2}-t_{1})^{2}-(x_{2}-x_{1})^{2}=c^{2}(t_{2}'-t_{1}')^{2}-(x_{2}'-x_{1}')^{2}.$

Quyidagi misollarning aksariyatida standart konfiguratsiya qoʻllaniladi. Oddiyroq muammoning chiziqli yechimi

$(ct)^{2}-x^{2}=(ct')^{2}-x'^{2}$

umumiy muammoni hal qiladi, chunki koordinatalar farqlari xuddi shu tarzda oʻzgaradi. Lineerlik koʻpincha adabiyotda ushbu oddiyroq muammo koʻrib chiqilayotganda qandaydir tarzda taxmin qilinadi yoki muhokama qilinadi. Agar oddiyroq muammoning yechimi chiziqli boʻlmasa, kvadratlarni kengaytirishda koʻndalang atamalar paydo boʻlgani uchun u asl masalani hal qilmaydi.

Yechimlar

Yuqorida aytib oʻtilganidek, umumiy muammo fazodagi tarjimalar orqali hal qilinadi. Ular qoʻyilgan oddiyroq muammoning yechimi sifatida koʻrinmaydi, biroq kuchaytirgichlar (va baʼzan hujum burchagiga qarab aylanishlar). Agar faqat yorugʻlikka oʻxshash ajratilgan hodisalar uchun intervalning oʻzgarmasligini talab qilsa, yanada koʻproq echimlar mavjud. Bular chiziqli boʻlmagan konformal ("burchakni saqlaydigan") transformatsiyalardir. Birida bor.

Fizikaning baʼzi tenglamalari konformal invariantdir, masalan, manbasiz fazodagi Maksvell tenglamalari, lekin hammasi emas. Kosmosdagi konformal oʻzgarishlarning dolzarbligi hozircha maʼlum emas, lekin ikki oʻlchovdagi konformal guruh konformal maydon nazariyasi va statistik mexanikada juda dolzarbdir. Shunday qilib, maxsus nisbiylik postulatlari tomonidan alohida ajratilgan Puankare guruhidir. Bu uni Galiley nisbiyligining Galiley guruhidan ajratib turadigan oddiy kuchaytirgichlardan farqli oʻlaroq, Lorentz kuchaytirgichlarining mavjudligi (buning uchun tezlikni qoʻshish yorugʻlik tezligidan kattaroq tezlikni taʼminlaydigan oddiy vektor qoʻshilishidan farq qiladi). Fazoviy aylanishlar, fazoviy va vaqtinchalik inversiyalar va tarjimalar ikkala guruhda ham mavjud va ikkala nazariyada ham bir xil oqibatlarga olib keladi (impuls, energiya va burchak momentumining saqlanish qonunlari). Hamma qabul qilingan nazariyalar inversiya ostidagi simmetriyani hurmat qilmaydi.

Fazoviy vaqt geometriyasidan foydalanish

Landau va Lifshitz yechimi

Ushbu uchta giperbolik funksiya formulalari (H1 – H3) quyida keltirilgan:

1. $\cosh ^{2}\Psi -\sinh ^{2}\Psi =1,$
2. $\sinh \Psi ={\frac {\tanh \Psi }{\sqrt {1-\tanh ^{2}\Psi }}},$
3. $\cosh \Psi ={\frac {1}{\sqrt {1-\tanh ^{2}\Psi }}},$

Astarlangan koordinatalar harakatlanuvchi tizimga tegishli boʻlgan x-direction kuchaytirish uchun standart konfiguratsiyada qoʻyilgan muammo oddiyroq muammoning chiziqli echimini topish orqali hal qilinadi.

$(ct)^{2}-x^{2}=(ct')^{2}-x'^{2}.$

Eng umumiy yechim, (H1) yordamida toʻgʻridan-toʻgʻri almashtirish orqali tasdiqlanishi mumkin,

$x=x'\cosh \Psi +ct'\sinh \Psi ,\quad ct=x'\sinh \Psi +ct'\cosh \Psi .$ $x=x'\cosh \Psi +ct'\sinh \Psi ,\quad ct=x'\sinh \Psi +ct'\cosh \Psi .$

Ψ ning jismoniy sharoitdagi rolini topish uchun F′ ning kelib chiqishi progressiyasini yozing, yaʼni x′ = 0, x = vt . Tenglamalar boʻladi (birinchi x′ = 0 dan foydalangan holda),

$x=ct'sinh\Psi ,\quad ct=ct'cosh\Psi .$

Endi ajrating:

${\frac {x}{ct}}=\tanh \Psi ={\frac {v}{c}}\Rightarrow \quad \sinh \Psi ={\frac {\frac {v}{c}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}},\quad \cosh \Psi ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}},$

Bu yerda birinchi bosqichda x = vt, ikkinchisida (H2) va (H3) ishlatilgan, bu esa qayta ulanganda (1) beradi

$x={\frac {x'+vt'}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}},\quad t={\frac {t'+{\frac {v}{c^{2}}}x'}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}},$

yoki odatdagi qisqartmalar bilan,

$x=\gamma (x'+vt'),\,\,t=\gamma \left(t'+{\frac {vx'}{c^{2}}}\right),\quad x'=\gamma (x-vt),\,\,t'=\gamma \left(t-{\frac {vx}{c^{2}}}\right).$

Manbalar

• Greiner, W.; Bromley, D. A.. Relativistic Quantum Mechanics, 3rd, springer, 2000. ISBN 9783540674573. 
• Landau, L.D.; Lifshitz, E.M.. The Classical Theory of Fields, 4th, Course of Theoretical Physics, Butterworth–Heinemann, 2002. ISBN 0-7506-2768-9. 
• Weinberg, S. (2002), The Quantum Theory of Fields, 1-jild, Cambridge University Press, ISBN 0-521-55001-7