Massa markazi: Versiyalar orasidagi farq
„Center of mass“ sahifasi tarjima qilib yaratildi |
yangi |
||
| Qator 1: | Qator 1: | ||
[[Fayl:Bird_toy_showing_center_of_gravity.jpg|thumb| Ushbu oʻyinchoq barmoq ustida oʻtirganda muvozanatni saqlash uchun massa markazi tamoyillaridan foydalanadi.]] |
|||
Fizikada kosmosda [[massa]] taqsimotining '''massa markazi''' (baʼzan '''muvozanat nuqtasi''' deb ataladi) har qanday vaqtda taqsimlangan massaning nisbiy [[Holat (geometriya)|pozitsiyasi]] nolga teng boʻlgan yagona nuqtadir. Bu [[Burchak tezlanish|burchak tezlashuvisiz]] [[Tezlanish|chiziqli tezlanishni]] keltirib chiqaradigan kuch qoʻllanilishi mumkin boʻlgan nuqtadir. [[Mexanika|Mexanikadagi]] hisob-kitoblar koʻpincha massa markaziga nisbatan tuzilganda soddalashtiriladi. Bu ob’ektning butun massasi uning harakatini tasavvur qilish uchun toʻplangan deb taxmin qilinadigan faraziy nuqtadir. Boshqacha qilib aytganda, massa markazi [[Newton qonunlari|Nyutonning harakat qonunlarini]] qoʻllash uchun berilgan ob’ektning zarracha ekvivalentidir. |
|||
Yagona qattiq jism boʻlsa, massa markazi tanaga nisbatan oʻrnatiladi va agar tana bir xil zichlikka ega boʻlsa, u markazda joylashgan boʻladi. Massa markazi jismoniy tanadan tashqarida joylashgan boʻlishi mumkin, baʼzida [[wiktionary:hollow|ichi boʻsh]] yoki ochiq shakldagi narsalar, masalan, [[taqa]] . [[Quyosh tizimi|Quyosh tizimining]] [[Sayyora|sayyoralari]] kabi alohida jismlarning taqsimlanishida massa markazi tizimning biron bir alohida aʼzosining pozitsiyasiga mos kelmasligi mumkin. |
|||
[[Fayl:Bird_toy_showing_center_of_gravity.jpg|thumb| Ushbu o'yinchoq barmoq ustida o'tirganda muvozanatni saqlash uchun massa markazi tamoyillaridan foydalanadi.]] |
|||
Fizikada kosmosda [[massa]] taqsimotining '''massa markazi''' (ba'zan '''muvozanat nuqtasi''' deb ataladi) har qanday vaqtda taqsimlangan massaning nisbiy [[Holat (geometriya)|pozitsiyasi]] nolga teng bo'lgan yagona nuqtadir. Bu [[Burchak tezlanish|burchak tezlashuvisiz]] [[Tezlanish|chiziqli tezlanishni]] keltirib chiqaradigan kuch qo'llanilishi mumkin bo'lgan nuqtadir. [[Mexanika|Mexanikadagi]] hisob-kitoblar ko'pincha massa markaziga nisbatan tuzilganda soddalashtiriladi. Bu ob'ektning butun massasi uning harakatini tasavvur qilish uchun to'plangan deb taxmin qilinadigan faraziy nuqtadir. Boshqacha qilib aytganda, massa markazi [[Newton qonunlari|Nyutonning harakat qonunlarini]] qo'llash uchun berilgan ob'ektning zarracha ekvivalentidir. |
|||
Yagona qattiq jism bo'lsa, massa markazi tanaga nisbatan o'rnatiladi va agar tana bir xil zichlikka ega bo'lsa, u markazda joylashgan bo'ladi. Massa markazi jismoniy tanadan tashqarida joylashgan bo'lishi mumkin, ba'zida [[wiktionary:hollow|ichi bo'sh]] yoki ochiq shakldagi narsalar, masalan, [[taqa]] . [[Quyosh tizimi|Quyosh tizimining]] [[Sayyora|sayyoralari]] kabi alohida jismlarning taqsimlanishida massa markazi tizimning biron bir alohida a'zosining pozitsiyasiga mos kelmasligi mumkin. |
|||
Massa markazi kosmosda tarqalgan massalarni, masalan, sayyora jismlarining [[Impuls|chiziqli]] va burchak impulslarini va qattiq jismlar dinamikasini o'z ichiga olgan [[Mexanika|mexanikada]] hisob-kitoblar uchun foydali mos yozuvlar nuqtasidir. [[Astrodinamika|Orbital mexanikada]] sayyoralar harakati tenglamalari massa markazlarida joylashgan [[Nuqtaviy zarra|nuqta massalari]] sifatida tuzilgan. Massa markazi - [[Inersial sanoq sistemasi|inertial tizim]] bo'lib, unda tizimning massa markazi koordinatalar tizimining boshiga nisbatan tinch holatda bo'ladi. |
|||
Massa markazi kosmosda tarqalgan massalarni, masalan, sayyora jismlarining [[Impuls|chiziqli]] va burchak impulslarini va qattiq jismlar dinamikasini oʻz ichiga olgan [[Mexanika|mexanikada]] hisob-kitoblar uchun foydali mos yozuvlar nuqtasidir. [[Astrodinamika|Orbital mexanikada]] sayyoralar harakati tenglamalari massa markazlarida joylashgan [[Nuqtaviy zarra|nuqta massalari]] sifatida tuzilgan. Massa markazi — [[Inersial sanoq sistemasi|inertial tizim]] boʻlib, unda tizimning massa markazi koordinatalar tizimining boshiga nisbatan tinch holatda boʻladi. |
|||
== Tarix == |
== Tarix == |
||
Ogʻirlik markazi yoki ogʻirlik tushunchasi qadimgi yunon matematigi, fizigi va muhandisi [[Arximed|Sirakuzalik Arximed]] tomonidan keng oʻrganilgan. U bir xil maydonni tashkil etadigan tortishish haqidagi soddalashtirilgan taxminlar bilan ishladi va shu bilan biz hozir massa markazi deb ataydigan narsaning matematik xususiyatlariga erishdi. Arximed, [[Richag|tutqichning]] turli nuqtalarida joylashgan ogʻirliklar tomonidan dastakka taʼsir qilish momenti, agar barcha ogʻirliklar bitta nuqtaga — ularning massa markaziga koʻchirilganda qanday boʻlishini koʻrsatdi. Arximed oʻzining ''"Suzib yuruvchi jismlar haqida'' " asarida suzuvchi jismning yoʻnalishi uning massa markazini iloji boricha pastroq qiladigan narsa ekanligini koʻrsatdi. U har xil aniq shakldagi bir xil zichlikdagi jismlarning massa markazlarini topishning matematik usullarini ishlab chiqdi. {{Sfn|Shore|2008}} |
|||
Massa markazi nazariyasiga hissa |
Massa markazi nazariyasiga hissa qoʻshgan boshqa qadimgi matematiklar orasida [[Geron|Iskandariya Qahramoni]] va [[Iskandariya pappasi|Iskandariya Pappus]] ham bor. Uygʻonish va Ilk zamonaviy davrlarda Gvido Ubaldi, Franchesko Mauroliko, {{Sfn|Baron|2004}} Federiko Komandino, {{Sfn|Baron|2004}} [[Evangelista Torricelli]], Simon Stevin, {{Sfn|Baron|2004}} Luka Valerio, {{Sfn|Baron|2004}} Jan-Sharl de la Fail, Pol Guldin, {{Sfn|Mancosu|1999}} [[John Wallis|Jon Uollis]], [[Christiaan Huygens|Kristian Gyuygens]], <ref>{{Cite journal|last=Erlichson|first1=H.|date=1996|title=Christiaan Huygens' discovery of the center of oscillation formula|url=https://aapt.scitation.org/doi/10.1119/1.18156|journal=American Journal of Physics|volume=64|issue=5|pages=571–574|doi=10.1119/1.18156|bibcode=1996AmJPh..64..571E|issn=0002-9505}}</ref> Lui Karre, [[Varinyon Pyer|Per Varinyon]] va Aleksis Kler kontseptsiyani yanada kengaytirdilar. {{Sfn|Walton|1855}} |
||
[[Newton qonunlari|Nyutonning ikkinchi qonuni]] Eylerning birinchi qonunida massalar markaziga nisbatan qayta tuzilgan. {{Sfn|Beatty|2006}} |
[[Newton qonunlari|Nyutonning ikkinchi qonuni]] Eylerning birinchi qonunida massalar markaziga nisbatan qayta tuzilgan. {{Sfn|Beatty|2006}} |
||
== Taʼrif == |
|||
Massa markazi kosmosda massa taqsimoti markazidagi yagona nuqta boʻlib, bu nuqtaga nisbatan ogʻirlikli pozitsiya vektorlarini nolga tenglashtiradigan xususiyatga ega. Statistikaga oʻxshab, massa markazi kosmosda massa taqsimotining oʻrtacha joylashuvidir. |
|||
== |
=== Zarrachalar tizimi === |
||
Massa markazi kosmosda massa taqsimoti markazidagi yagona nuqta bo'lib, bu nuqtaga nisbatan og'irlikli pozitsiya vektorlarini nolga tenglashtiradigan xususiyatga ega. Statistikaga o'xshab, massa markazi kosmosda massa taqsimotining o'rtacha joylashuvidir. |
|||
Koordinatalari {{Math|1=''P<sub>i</sub>'', ''i'' = 1, ..., ''n'' }} fazoda joylashgan har birining massasi {{Mvar|m<sub>i</sub>}} boʻlgan {{Math|1='''r'''<sub>''i''</sub>, ''i'' = 1, ..., ''n'' }} zarralar sistemasida koordinatalar '''R''' ning koordinatalari. massa markazi shartni qondiradi: |
|||
Zarrachalar tizimi |
|||
Koordinatalari {{Math|1=''P<sub>i</sub>'', ''i'' = 1, ..., ''n'' }} fazoda joylashgan har birining massasi {{Mvar|m<sub>i</sub>}} bo‘lgan {{Math|1='''r'''<sub>''i''</sub>, ''i'' = 1, ..., ''n'' }} zarralar sistemasida koordinatalar '''R''' ning koordinatalari. massa markazi shartni qondiradi: |
|||
\sum_{i=1}^n m_i(\mathbf{r}_i - \mathbf{R}) = \mathbf{0}. |
|||
<math>\sum_{i=1}^n m_i(\mathbf{r}_i - \mathbf{R}) = \mathbf{0}.</math> |
|||
'''R''' uchun bu tenglamani yechish formulani beradi: |
'''R''' uchun bu tenglamani yechish formulani beradi: |
||
\mathbf{R} = \frac 1M \sum_{i=1}^n m_i \mathbf{r}_i, |
<math>\mathbf{R} = \frac 1M \sum_{i=1}^n m_i \mathbf{r}_i,</math> |
||
bu yerda <math> M = \sum_{i = 1}^n m_i </math> barcha zarrachalarning umumiy massasi. |
bu yerda <math> M = \sum_{i = 1}^n m_i </math> barcha zarrachalarning umumiy massasi. |
||
=== |
=== Oʻzgarmas hajm === |
||
Agar massa taqsimoti qattiq ''Q'' ichida r( |
Agar massa taqsimoti qattiq ''Q'' ichida r('''r''') zichligi bilan uzluksiz boʻlsa, u holda bu hajmdagi nuqtalarning '''R''' massa markaziga nisbatan '''V''' hajmdagi vaznli joylashuv koordinatalarining integrali nolga teng, yaʼni |
||
\iiint_{Q} \rho(\mathbf{r}) \left(\mathbf{r} - \mathbf{R}\right) dV = 0. |
<math>\iiint_{Q} \rho(\mathbf{r}) \left(\mathbf{r} - \mathbf{R}\right) dV = 0.</math> |
||
'''R''' qiymat olish uchun koordinatalari uchun ushbu tenglamani yechamiz: |
'''R''' qiymat olish uchun koordinatalari uchun ushbu tenglamani yechamiz: |
||
\mathbf R = \frac 1 M \iiint_{Q}\rho(\mathbf{r}) \mathbf{r} \, dV, |
<math>\mathbf R = \frac 1 M \iiint_{Q}\rho(\mathbf{r}) \mathbf{r} \, dV,</math> |
||
bu yerda M |
bu yerda M — hajmdagi umumiy massa. |
||
Agar uzluksiz massa taqsimoti bir xil zichlikka ega |
Agar uzluksiz massa taqsimoti bir xil zichlikka ega boʻlsa, yaʼni ''r'' doimiy boʻlsa, u holda massa markazi hajmning markazi bilan bir xil boʻladi. {{Sfn|Levi|2009}} |
||
=== Barisentrik koordinatalar === |
=== Barisentrik koordinatalar === |
||
Massalari ''m'' <sub>1</sub> va ''m'' <sub>2</sub> |
Massalari ''m'' <sub>1</sub> va ''m'' <sub>2</sub> boʻlgan ''P'' <sub>1</sub> va ''P'' <sub>2</sub> boʻlgan ikki zarrali sistemaning massalar markazining '''R''' koordinatalari quyidagicha ifodalanadi: |
||
\mathbf{R} = \frac{1}{m_1 + m_2}(m_1 \mathbf{r}_1 + m_2\mathbf{r}_2). |
<math>\mathbf{R} = \frac{1}{m_1 + m_2}(m_1 \mathbf{r}_1 + m_2\mathbf{r}_2).</math> |
||
Bu ikki zarracha |
Bu ikki zarracha oʻrtasida boʻlingan umumiy massaning foizi 100% ''P'' <sub>1</sub> va 0% ''P'' <sub>2</sub> dan 50% ''P'' <sub>1</sub> va 50% ''P'' <sub>2</sub> dan 0% ''P'' <sub>1</sub> va 100% ''P'' <sub>2</sub> gacha, keyin massa markazi '''R''' boʻlsin. ''P'' <sub>1</sub> dan ''P'' <sub>2</sub> gacha boʻlgan chiziq boʻylab harakatlanadi. Har bir nuqtadagi massa foizlarini ushbu chiziqdagi '''R''' nuqtaning proyektiv koordinatalari sifatida koʻrish mumkin va ular barisentrik koordinatalar deb ataladi. Bu erda jarayonni izohlashning yana bir usuli — ixtiyoriy nuqtaga nisbatan momentlarni mexanik muvozanatlash. Numerator massa markazida ekvivalent umumiy kuch bilan muvozanatlangan umumiy momentni beradi. Buni tekislikda va fazoda proyektiv koordinatalarni aniqlash uchun uch nuqta va toʻrt nuqtaga umumlashtirish mumkin. |
||
=== Davriy chegara shartlariga ega tizimlar === |
=== Davriy chegara shartlariga ega tizimlar === |
||
Davriy chegaraviy shartlarga ega |
Davriy chegaraviy shartlarga ega boʻlgan tizimdagi zarralar uchun ikkita zarra tizimning qarama-qarshi tomonlarida boʻlsa ham, qoʻshni boʻlishi mumkin. Bu koʻpincha molekulyar dinamika simulyatsiyalarida sodir boʻladi, masalan, klasterlar tasodifiy joylarda hosil boʻladi va baʼzan qoʻshni atomlar davriy chegarani kesib oʻtadi. Klaster davriy chegarani kesib oʻtganda, massa markazini sodda hisoblash notoʻgʻri boʻladi. Davriy tizimlar uchun massa markazini hisoblashning umumlashtirilgan usuli har bir koordinatani, ''x'', ''y'' va/yoki ''z ni'' chiziq oʻrniga aylanada boʻlgandek koʻrib chiqishdir. {{Sfn|Bai|Breen|2008}} Hisoblash har bir zarrachaning ''x'' koordinatasini oladi va uni burchakka chizadi, |
||
\theta_i = \frac{x_i}{x_\max} 2 \pi |
<math>\theta_i = \frac{x_i}{x_\max} 2 \pi</math> |
||
bu yerda ''x'' <sub>max</sub> |
bu yerda ''x'' <sub>max</sub> — ''x'' yoʻnalishidagi tizim hajmi va <math>x_i \in [0, x_\max)</math> . Shu nuqtai nazardan, ikkita yangi nuqta <math>(\xi_i, \zeta_i)</math> hosil boʻlishi mumkin, bu zarrachaning massasi bilan tortilishi mumkin <math>x_i</math> massa markazi uchun yoki geometrik markaz uchun 1 qiymati berilgan: |
||
\begin{align} |
<math display="block">\begin{align} |
||
\xi_i &= \cos(\theta_i) \\ |
|||
\zeta_i &= \sin(\theta_i) |
|||
\end{align}</math> |
|||
<math>(\xi, \zeta)</math> tekislikda, bu koordinatalar radiusi 1 boʻlgan doirada yotadi. kolleksiyasidan <math>\xi_i</math> va <math>\zeta_i</math> barcha zarralardan olingan qiymatlar, oʻrtachalar <math>\overline{\xi}</math> va <math>\overline{\zeta}</math> hisoblab chiqiladi. |
|||
\xi_i &= \cos(\theta_i) \\ |
|||
<math display="block">\begin{align} |
|||
\zeta_i &= \sin(\theta_i) |
|||
\overline{\xi} &= \frac 1 M \sum_{i=1}^n m_i \xi_i, \\ |
|||
\overline{\zeta} &= \frac 1 M \sum_{i=1}^n m_i \zeta_i, |
|||
\end{align}</math> |
|||
Bu yerda {{Mvar|M}} — barcha zarrachalarning massalari yigʻindisi. |
|||
\end{align} |
|||
Ushbu qiymatlar yangi burchak ostida qayta koʻrib chiqiladi, <math>\overline{\theta}</math>, undan massa markazining ''x'' koordinatasini olish mumkin: |
|||
<math display="block">\begin{align} |
|||
In <math>(\xi, \zeta)</math> tekislikda, bu koordinatalar radiusi 1 bo'lgan doirada yotadi. kolleksiyasidan <math>\xi_i</math> va <math>\zeta_i</math> barcha zarralardan olingan qiymatlar, o'rtachalar <math>\overline{\xi}</math> va <math>\overline{\zeta}</math> hisoblab chiqiladi. |
|||
\overline{\theta} &= \operatorname{atan2}\left(-\overline{\zeta}, -\overline{\xi}\right) + \pi \\ |
|||
x_\text{com} &= x_\max \frac{\overline{\theta}}{2 \pi} |
|||
\end{align}</math> |
|||
Toʻliq massa markazini aniqlash uchun jarayon tizimning barcha oʻlchamlari uchun takrorlanishi mumkin. Algoritmning foydali tomoni shundaki, u matematikaga davriy chegaralarni bosib oʻtuvchi klasterni „ochish“ uchun taxmin qilish yoki klaster tahlilidan foydalanish oʻrniga „eng yaxshi“ massa markazi qayerda ekanligini aniqlash imkonini beradi. Agar ikkala oʻrtacha qiymat nolga teng boʻlsa, <math>\left(\overline{\xi}, \overline{\zeta}\right) = (0, 0)</math>, keyin <math>\overline{\theta}</math> aniqlanmagan. Bu toʻgʻri natijadir, chunki u faqat barcha zarralar bir tekisda joylashganda paydo boʻladi. Bunday holda, ularning ''x'' koordinatalari davriy tizimda matematik jihatdan bir xil boʻladi. |
|||
\begin{align} |
|||
== Ogʻirlik markazi == |
|||
\overline{\xi} &= \frac 1 M \sum_{i=1}^n m_i \xi_i, \\ |
|||
[[Fayl:CoG_stable.svg|thumb| Bir nuqtada muvozanatni saqlaydigan oʻquv oʻyinchoqlarining diagrammasi: massa markazi (C) uning tayanchidan § pastga joylashadi.]] |
|||
Jismning ogʻirlik markazi — tortishish kuchlari taʼsirida hosil boʻlgan moment yoʻqolgan nuqta. Ogʻirlik maydonini bir xil deb hisoblash mumkin boʻlgan joyda, massa markazi va ogʻirlik markazi bir xil boʻladi. Biroq, sayyora atrofida orbitadagi sunʼiy yoʻldoshlar uchun, sunʼiy yoʻldoshga qoʻllaniladigan boshqa momentlar boʻlmasa, tortishish maydonining sayyoraga yaqinroq (kuchliroq) va uzoqroq (zaifroq) oʻrtasidagi ozgina oʻzgarishi (gradient) sunʼiy yoʻldoshni uning uzun oʻqi vertikal boʻlishi uchun tekislashga moyil boʻlgan moment. Bunday holda, ogʻirlik markazi va massa markazi oʻrtasidagi farqni aniqlash muhimdir. Ikkalasi orasidagi har qanday gorizontal siljish qoʻllaniladigan momentga olib keladi. |
|||
Shuni taʼkidlash kerakki, massa markazi maʼlum bir qattiq jism uchun sobit xususiyatdir (masalan, egilishsiz yoki artikulyatsiyasiz), ogʻirlik markazi esa, qoʻshimcha ravishda, uning bir xil boʻlmagan tortishish kuchida yoʻnalishiga bogʻliq boʻlishi mumkin. maydon. Ikkinchi holda, ogʻirlik markazi har doim asosiy jozibali jismga massa markaziga nisbatan bir oz yaqinroq joylashgan boʻladi va shuning uchun uning yoʻnalishi oʻzgarganda, qiziqish jismidagi oʻrnini oʻzgartiradi. |
|||
\overline{\zeta} &= \frac 1 M \sum_{i=1}^n m_i \zeta_i, |
|||
Samolyotlar, transport vositalari va kemalar dinamikasini oʻrganishda kuchlar va momentlarni massa markaziga nisbatan hal qilish kerak. Bu tortishishning oʻzi eʼtiborga olinishidan qatʼi nazar, haqiqatdir. Ogʻirlik markazi sifatida massa markaziga murojaat qilish soʻzlashuv tilidir, lekin u umumiy qoʻllaniladi va tortishish gradient effektlari ahamiyatsiz boʻlsa, ogʻirlik markazi va massa markazi bir xil boʻladi va bir-birining oʻrnida ishlatiladi. |
|||
\end{align} |
|||
Fizikada massa taqsimotini modellashtirish uchun massa markazidan foydalanishning afzalliklarini uzluksiz tanadagi tortishish kuchlarining natijasini hisobga olgan holda koʻrish mumkin. Hajmning '''har''' bir nuqtasida ''r'' ('''r''') zichligi ''V'' hajmli ''Q'' jismni koʻrib chiqaylik. Parallel tortishish maydonida har bir '''r''' nuqtadagi '''f''' kuchi quyidagicha ifodalanadi: |
|||
Bu yerda {{Mvar|M}} - barcha zarrachalarning massalari yig'indisi. |
|||
<math>\mathbf{f}(\mathbf{r}) = -dm\, g\mathbf{\hat{k}} = -\rho(\mathbf{r}) \, dV\,g\mathbf{\hat{k}},</math> |
|||
Ushbu qiymatlar yangi burchak ostida qayta ko'rib chiqiladi, <math>\overline{\theta}</math>, undan massa markazining ''x'' koordinatasini olish mumkin: |
|||
Bu yerda ''dm'' — '''r''' nuqtadagi massa, ''g'' — tortishish tezlashishi va <math display="inline">\mathbf{\hat{k}}</math> — vertikal yoʻnalishni belgilovchi birlik vektor. |
|||
\begin{align} |
|||
Ovoz hajmida mos yozuvlar nuqtasi '''R''' ni tanlang va shu nuqtada hosil boʻlgan kuch va momentni hisoblaymiz: |
|||
\overline{\theta} &= \operatorname{atan2}\left(-\overline{\zeta}, -\overline{\xi}\right) + \pi \\ |
|||
<math>\mathbf{F} = \iiint_{Q} \mathbf{f}(\mathbf{r}) \, dV = \iiint_{Q}\rho(\mathbf{r}) \, dV \left( -g \mathbf{\hat{k}}\right) = -Mg\mathbf{\hat{k}},</math> |
|||
<nowiki> x_\text{com} &= x_\max \frac{\overline{\theta}}{2 \pi}</nowiki> |
|||
va |
|||
\end{align} |
|||
<math display="block" qid="Q48103"> \mathbf{T} = \iiint_{Q} (\mathbf{r} - \mathbf{R}) \times \mathbf{f}(\mathbf{r}) \, dV = \iiint_{Q} (\mathbf{r} - \mathbf{R}) \times \left(-g\rho(\mathbf{r}) \, dV \, \mathbf{\hat{k}}\right) = \left(\iiint_{Q} \rho(\mathbf{r}) \left(\mathbf{r} - \mathbf{R}\right) dV \right) \times \left(-g\mathbf{\hat{k}}\right) .</math> |
|||
To'liq massa markazini aniqlash uchun jarayon tizimning barcha o'lchamlari uchun takrorlanishi mumkin. Algoritmning foydali tomoni shundaki, u matematikaga davriy chegaralarni bosib o'tuvchi klasterni "ochish" uchun taxmin qilish yoki klaster tahlilidan foydalanish o'rniga "eng yaxshi" massa markazi qayerda ekanligini aniqlash imkonini beradi. Agar ikkala o'rtacha qiymat nolga teng bo'lsa, <math>\left(\overline{\xi}, \overline{\zeta}\right) = (0, 0)</math>, keyin <math>\overline{\theta}</math> aniqlanmagan. Bu to'g'ri natijadir, chunki u faqat barcha zarralar bir tekisda joylashganda paydo bo'ladi. Bunday holda, ularning ''x'' koordinatalari davriy tizimda matematik jihatdan bir xil bo'ladi. |
|||
== Og'irlik markazi == |
|||
[[Fayl:CoG_stable.svg|thumb| Bir nuqtada muvozanatni saqlaydigan o'quv o'yinchoqlarining diagrammasi: massa markazi (C) uning tayanchidan (P) pastga joylashadi.]] |
|||
Jismning og'irlik markazi - tortishish kuchlari ta'sirida hosil bo'lgan moment yo'qolgan nuqta. Og'irlik maydonini bir xil deb hisoblash mumkin bo'lgan joyda, massa markazi va og'irlik markazi bir xil bo'ladi. Biroq, sayyora atrofida orbitadagi sun'iy yo'ldoshlar uchun, sun'iy yo'ldoshga qo'llaniladigan boshqa momentlar bo'lmasa, tortishish maydonining sayyoraga yaqinroq (kuchliroq) va uzoqroq (zaifroq) o'rtasidagi ozgina o'zgarishi (gradient) sun'iy yo'ldoshni uning uzun o'qi vertikal bo'lishi uchun tekislashga moyil bo'lgan moment. Bunday holda, og'irlik markazi va massa markazi o'rtasidagi farqni aniqlash muhimdir. Ikkalasi orasidagi har qanday gorizontal siljish qo'llaniladigan momentga olib keladi. |
|||
Shuni ta'kidlash kerakki, massa markazi ma'lum bir qattiq jism uchun sobit xususiyatdir (masalan, egilishsiz yoki artikulyatsiyasiz), og'irlik markazi esa, qo'shimcha ravishda, uning bir xil bo'lmagan tortishish kuchida yo'nalishiga bog'liq bo'lishi mumkin. maydon. Ikkinchi holda, og'irlik markazi har doim asosiy jozibali jismga massa markaziga nisbatan bir oz yaqinroq joylashgan bo'ladi va shuning uchun uning yo'nalishi o'zgarganda, qiziqish jismidagi o'rnini o'zgartiradi. |
|||
Samolyotlar, transport vositalari va kemalar dinamikasini o'rganishda kuchlar va momentlarni massa markaziga nisbatan hal qilish kerak. Bu tortishishning o'zi e'tiborga olinishidan qat'i nazar, haqiqatdir. Og'irlik markazi sifatida massa markaziga murojaat qilish so'zlashuv tilidir, lekin u umumiy qo'llaniladi va tortishish gradient effektlari ahamiyatsiz bo'lsa, og'irlik markazi va massa markazi bir xil bo'ladi va bir-birining o'rnida ishlatiladi. |
|||
Fizikada massa taqsimotini modellashtirish uchun massa markazidan foydalanishning afzalliklarini uzluksiz tanadagi tortishish kuchlarining natijasini hisobga olgan holda ko'rish mumkin. Hajmning '''har''' bir nuqtasida ''r'' ( '''r''' ) zichligi ''V'' hajmli ''Q'' jismni ko'rib chiqaylik. Parallel tortishish maydonida har bir '''r''' nuqtadagi '''f''' kuchi quyidagicha ifodalanadi: |
|||
<nowiki>\mathbf{f}(\mathbf{r}) = -dm\, g\mathbf{\hat{k}} = -\rho(\mathbf{r}) \, dV\,g\mathbf{\hat{k}},</nowiki> |
|||
Bu yerda ''dm'' - '''r''' nuqtadagi massa, ''g'' - tortishish tezlashishi va <math display="inline">\mathbf{\hat{k}}</math> - vertikal yo'nalishni belgilovchi birlik vektor. |
|||
Ovoz hajmida mos yozuvlar nuqtasi '''R''' ni tanlang va shu nuqtada hosil bo'lgan kuch va momentni hisoblaymiz: |
|||
<nowiki>\mathbf{F} = \iiint_{Q} \mathbf{f}(\mathbf{r}) \, dV = \iiint_{Q}\rho(\mathbf{r}) \, dV \left( -g \mathbf{\hat{k}}\right) = -Mg\mathbf{\hat{k}},</nowiki> |
|||
va |
|||
Agar '''R''' mos yozuvlar nuqtasi massa markazi boʻlishi uchun tanlansa, u holda |
|||
<nowiki>\mathbf{T} = \iiint_{Q} (\mathbf{r} - \mathbf{R}) \times \mathbf{f}(\mathbf{r}) \, dV = \iiint_{Q} (\mathbf{r} - \mathbf{R}) \times \left(-g\rho(\mathbf{r}) \, dV \, \mathbf{\hat{k}}\right) = \left(\iiint_{Q} \rho(\mathbf{r}) \left(\mathbf{r} - \mathbf{R}\right) dV \right) \times \left(-g\mathbf{\hat{k}}\right) .</nowiki> |
|||
<math>\iiint_{Q} \rho(\mathbf{r}) \left(\mathbf{r} - \mathbf{R}\right) dV = 0,</math> |
|||
Agar '''R''' mos yozuvlar nuqtasi massa markazi bo'lishi uchun tanlansa, u holda |
|||
natijada olingan moment {{Nobr|1='''T''' = 0}} ni bildiradi. Natijada paydo boʻlgan moment nolga teng boʻlganligi sababli, tana massasi massa markazida toʻplangan zarra kabi harakat qiladi. |
|||
\iiint_{Q} \rho(\mathbf{r}) \left(\mathbf{r} - \mathbf{R}\right) dV = 0, |
|||
Ogʻirlik markazini qattiq jism uchun mos yozuvlar nuqtasi sifatida tanlab, tortishish kuchlari tananing aylanishiga olib kelmaydi, yaʼni tananing ogʻirligi massa markazida toʻplangan deb hisoblash mumkin. |
|||
natijada olingan moment {{Nobr|1='''T''' = 0}} ni bildiradi. Natijada paydo bo'lgan moment nolga teng bo'lganligi sababli, tana massasi massa markazida to'plangan zarra kabi harakat qiladi. |
|||
{{Reflist}} |
|||
Og'irlik markazini qattiq jism uchun mos yozuvlar nuqtasi sifatida tanlab, tortishish kuchlari tananing aylanishiga olib kelmaydi, ya'ni tananing og'irligi massa markazida to'plangan deb hisoblash mumkin. |
|||
== Manbalar == |
|||
* {{Citation |last=Asimov |first=Isaac |author-link=Isaac Asimov |date=1988 |orig-year=1966 |title=Understanding Physics |publisher=Barnes & Noble Books |isbn=978-0-88029-251-1|title-link=Understanding Physics }} |
|||
* {{cite journal |last1=Bai |first1=Linge |last2=Breen |first2=David |date=2008 |title=Calculating Center of Mass in an Unbounded 2D Environment |journal=Journal of Graphics, GPU, and Game Tools |volume=13 |issue=4 |pages=53–60 |doi=10.1080/2151237X.2008.10129266 |s2cid=40807367}} |
|||
* {{Citation |last=Baron |first=Margaret E.|author-link=Margaret Baron |date=2004 |orig-year=1969 |title=The Origins of the Infinitesimal Calculus |publisher=Courier Dover Publications |isbn=978-0-486-49544-6}} |
|||
* {{Citation |last=Beatty |first=Millard F. |date=2006 |title=Principles of Engineering Mechanics, Volume 2: Dynamics—The Analysis of Motion |publisher=Springer |series=Mathematical Concepts and Methods in Science and Engineering |volume=33 |isbn=978-0-387-23704-6}} |
|||
* {{Citation |last=De Silva |first=Clarence W. |date=2002 |title=Vibration and shock handbook |publisher=CRC Press |isbn=978-0-8493-1580-0}} |
|||
* {{Citation |author=Federal Aviation Administration |author-link=Federal Aviation Administration |date=2007 |title=Aircraft Weight and Balance Handbook |publisher=[[United States Government Printing Office]] |url=http://www.faa.gov/library/manuals/aircraft/media/FAA-H-8083-1A.pdf |access-date=23 October 2011 |url-status=dead |archive-url=https://web.archive.org/web/20111019122246/http://www.faa.gov/library/manuals/aircraft/media/FAA-H-8083-1A.pdf |archive-date=19 October 2011 }} |
|||
* {{Citation |last1=Feynman |first1=Richard |author-link=Richard Feynman |last2=Leighton |first2=Robert B. |author2-link=Robert B. Leighton |last3=Sands |first3=Matthew |author3-link=Matthew Sands |date=1963 |title=The Feynman Lectures on Physics |volume=1 |edition=Sixth printing, February 1977 |publisher=Addison-Wesley |isbn=978-0-201-02010-6|title-link=The Feynman Lectures on Physics }} |
|||
[[Turkum:Mexanika]] |
[[Turkum:Mexanika]] |
||
3-Avgust 2023, 11:56 dagi (joriy) koʻrinishi

Fizikada kosmosda massa taqsimotining massa markazi (baʼzan muvozanat nuqtasi deb ataladi) har qanday vaqtda taqsimlangan massaning nisbiy pozitsiyasi nolga teng boʻlgan yagona nuqtadir. Bu burchak tezlashuvisiz chiziqli tezlanishni keltirib chiqaradigan kuch qoʻllanilishi mumkin boʻlgan nuqtadir. Mexanikadagi hisob-kitoblar koʻpincha massa markaziga nisbatan tuzilganda soddalashtiriladi. Bu ob’ektning butun massasi uning harakatini tasavvur qilish uchun toʻplangan deb taxmin qilinadigan faraziy nuqtadir. Boshqacha qilib aytganda, massa markazi Nyutonning harakat qonunlarini qoʻllash uchun berilgan ob’ektning zarracha ekvivalentidir.
Yagona qattiq jism boʻlsa, massa markazi tanaga nisbatan oʻrnatiladi va agar tana bir xil zichlikka ega boʻlsa, u markazda joylashgan boʻladi. Massa markazi jismoniy tanadan tashqarida joylashgan boʻlishi mumkin, baʼzida ichi boʻsh yoki ochiq shakldagi narsalar, masalan, taqa . Quyosh tizimining sayyoralari kabi alohida jismlarning taqsimlanishida massa markazi tizimning biron bir alohida aʼzosining pozitsiyasiga mos kelmasligi mumkin.
Massa markazi kosmosda tarqalgan massalarni, masalan, sayyora jismlarining chiziqli va burchak impulslarini va qattiq jismlar dinamikasini oʻz ichiga olgan mexanikada hisob-kitoblar uchun foydali mos yozuvlar nuqtasidir. Orbital mexanikada sayyoralar harakati tenglamalari massa markazlarida joylashgan nuqta massalari sifatida tuzilgan. Massa markazi — inertial tizim boʻlib, unda tizimning massa markazi koordinatalar tizimining boshiga nisbatan tinch holatda boʻladi.
Tarix[tahrir | manbasini tahrirlash]
Ogʻirlik markazi yoki ogʻirlik tushunchasi qadimgi yunon matematigi, fizigi va muhandisi Sirakuzalik Arximed tomonidan keng oʻrganilgan. U bir xil maydonni tashkil etadigan tortishish haqidagi soddalashtirilgan taxminlar bilan ishladi va shu bilan biz hozir massa markazi deb ataydigan narsaning matematik xususiyatlariga erishdi. Arximed, tutqichning turli nuqtalarida joylashgan ogʻirliklar tomonidan dastakka taʼsir qilish momenti, agar barcha ogʻirliklar bitta nuqtaga — ularning massa markaziga koʻchirilganda qanday boʻlishini koʻrsatdi. Arximed oʻzining "Suzib yuruvchi jismlar haqida " asarida suzuvchi jismning yoʻnalishi uning massa markazini iloji boricha pastroq qiladigan narsa ekanligini koʻrsatdi. U har xil aniq shakldagi bir xil zichlikdagi jismlarning massa markazlarini topishning matematik usullarini ishlab chiqdi. [1]
Massa markazi nazariyasiga hissa qoʻshgan boshqa qadimgi matematiklar orasida Iskandariya Qahramoni va Iskandariya Pappus ham bor. Uygʻonish va Ilk zamonaviy davrlarda Gvido Ubaldi, Franchesko Mauroliko, [2] Federiko Komandino, [2] Evangelista Torricelli, Simon Stevin, [2] Luka Valerio, [2] Jan-Sharl de la Fail, Pol Guldin, [3] Jon Uollis, Kristian Gyuygens, [4] Lui Karre, Per Varinyon va Aleksis Kler kontseptsiyani yanada kengaytirdilar. [5]
Nyutonning ikkinchi qonuni Eylerning birinchi qonunida massalar markaziga nisbatan qayta tuzilgan. [6]
Taʼrif[tahrir | manbasini tahrirlash]
Massa markazi kosmosda massa taqsimoti markazidagi yagona nuqta boʻlib, bu nuqtaga nisbatan ogʻirlikli pozitsiya vektorlarini nolga tenglashtiradigan xususiyatga ega. Statistikaga oʻxshab, massa markazi kosmosda massa taqsimotining oʻrtacha joylashuvidir.
Zarrachalar tizimi[tahrir | manbasini tahrirlash]
Koordinatalari Pi, i = 1, ..., n fazoda joylashgan har birining massasi mi boʻlgan ri, i = 1, ..., n zarralar sistemasida koordinatalar R ning koordinatalari. massa markazi shartni qondiradi:
R uchun bu tenglamani yechish formulani beradi:
bu yerda barcha zarrachalarning umumiy massasi.
Oʻzgarmas hajm[tahrir | manbasini tahrirlash]
Agar massa taqsimoti qattiq Q ichida r(r) zichligi bilan uzluksiz boʻlsa, u holda bu hajmdagi nuqtalarning R massa markaziga nisbatan V hajmdagi vaznli joylashuv koordinatalarining integrali nolga teng, yaʼni
R qiymat olish uchun koordinatalari uchun ushbu tenglamani yechamiz:
bu yerda M — hajmdagi umumiy massa.
Agar uzluksiz massa taqsimoti bir xil zichlikka ega boʻlsa, yaʼni r doimiy boʻlsa, u holda massa markazi hajmning markazi bilan bir xil boʻladi. [7]
Barisentrik koordinatalar[tahrir | manbasini tahrirlash]
Massalari m 1 va m 2 boʻlgan P 1 va P 2 boʻlgan ikki zarrali sistemaning massalar markazining R koordinatalari quyidagicha ifodalanadi:
Bu ikki zarracha oʻrtasida boʻlingan umumiy massaning foizi 100% P 1 va 0% P 2 dan 50% P 1 va 50% P 2 dan 0% P 1 va 100% P 2 gacha, keyin massa markazi R boʻlsin. P 1 dan P 2 gacha boʻlgan chiziq boʻylab harakatlanadi. Har bir nuqtadagi massa foizlarini ushbu chiziqdagi R nuqtaning proyektiv koordinatalari sifatida koʻrish mumkin va ular barisentrik koordinatalar deb ataladi. Bu erda jarayonni izohlashning yana bir usuli — ixtiyoriy nuqtaga nisbatan momentlarni mexanik muvozanatlash. Numerator massa markazida ekvivalent umumiy kuch bilan muvozanatlangan umumiy momentni beradi. Buni tekislikda va fazoda proyektiv koordinatalarni aniqlash uchun uch nuqta va toʻrt nuqtaga umumlashtirish mumkin.
Davriy chegara shartlariga ega tizimlar[tahrir | manbasini tahrirlash]
Davriy chegaraviy shartlarga ega boʻlgan tizimdagi zarralar uchun ikkita zarra tizimning qarama-qarshi tomonlarida boʻlsa ham, qoʻshni boʻlishi mumkin. Bu koʻpincha molekulyar dinamika simulyatsiyalarida sodir boʻladi, masalan, klasterlar tasodifiy joylarda hosil boʻladi va baʼzan qoʻshni atomlar davriy chegarani kesib oʻtadi. Klaster davriy chegarani kesib oʻtganda, massa markazini sodda hisoblash notoʻgʻri boʻladi. Davriy tizimlar uchun massa markazini hisoblashning umumlashtirilgan usuli har bir koordinatani, x, y va/yoki z ni chiziq oʻrniga aylanada boʻlgandek koʻrib chiqishdir. [8] Hisoblash har bir zarrachaning x koordinatasini oladi va uni burchakka chizadi,
bu yerda x max — x yoʻnalishidagi tizim hajmi va . Shu nuqtai nazardan, ikkita yangi nuqta hosil boʻlishi mumkin, bu zarrachaning massasi bilan tortilishi mumkin massa markazi uchun yoki geometrik markaz uchun 1 qiymati berilgan:
tekislikda, bu koordinatalar radiusi 1 boʻlgan doirada yotadi. kolleksiyasidan va barcha zarralardan olingan qiymatlar, oʻrtachalar va hisoblab chiqiladi.
Bu yerda M — barcha zarrachalarning massalari yigʻindisi.
Ushbu qiymatlar yangi burchak ostida qayta koʻrib chiqiladi, , undan massa markazining x koordinatasini olish mumkin:
Toʻliq massa markazini aniqlash uchun jarayon tizimning barcha oʻlchamlari uchun takrorlanishi mumkin. Algoritmning foydali tomoni shundaki, u matematikaga davriy chegaralarni bosib oʻtuvchi klasterni „ochish“ uchun taxmin qilish yoki klaster tahlilidan foydalanish oʻrniga „eng yaxshi“ massa markazi qayerda ekanligini aniqlash imkonini beradi. Agar ikkala oʻrtacha qiymat nolga teng boʻlsa, , keyin aniqlanmagan. Bu toʻgʻri natijadir, chunki u faqat barcha zarralar bir tekisda joylashganda paydo boʻladi. Bunday holda, ularning x koordinatalari davriy tizimda matematik jihatdan bir xil boʻladi.
Ogʻirlik markazi[tahrir | manbasini tahrirlash]
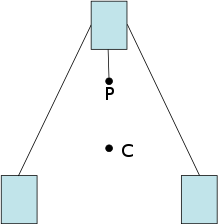
Jismning ogʻirlik markazi — tortishish kuchlari taʼsirida hosil boʻlgan moment yoʻqolgan nuqta. Ogʻirlik maydonini bir xil deb hisoblash mumkin boʻlgan joyda, massa markazi va ogʻirlik markazi bir xil boʻladi. Biroq, sayyora atrofida orbitadagi sunʼiy yoʻldoshlar uchun, sunʼiy yoʻldoshga qoʻllaniladigan boshqa momentlar boʻlmasa, tortishish maydonining sayyoraga yaqinroq (kuchliroq) va uzoqroq (zaifroq) oʻrtasidagi ozgina oʻzgarishi (gradient) sunʼiy yoʻldoshni uning uzun oʻqi vertikal boʻlishi uchun tekislashga moyil boʻlgan moment. Bunday holda, ogʻirlik markazi va massa markazi oʻrtasidagi farqni aniqlash muhimdir. Ikkalasi orasidagi har qanday gorizontal siljish qoʻllaniladigan momentga olib keladi.
Shuni taʼkidlash kerakki, massa markazi maʼlum bir qattiq jism uchun sobit xususiyatdir (masalan, egilishsiz yoki artikulyatsiyasiz), ogʻirlik markazi esa, qoʻshimcha ravishda, uning bir xil boʻlmagan tortishish kuchida yoʻnalishiga bogʻliq boʻlishi mumkin. maydon. Ikkinchi holda, ogʻirlik markazi har doim asosiy jozibali jismga massa markaziga nisbatan bir oz yaqinroq joylashgan boʻladi va shuning uchun uning yoʻnalishi oʻzgarganda, qiziqish jismidagi oʻrnini oʻzgartiradi.
Samolyotlar, transport vositalari va kemalar dinamikasini oʻrganishda kuchlar va momentlarni massa markaziga nisbatan hal qilish kerak. Bu tortishishning oʻzi eʼtiborga olinishidan qatʼi nazar, haqiqatdir. Ogʻirlik markazi sifatida massa markaziga murojaat qilish soʻzlashuv tilidir, lekin u umumiy qoʻllaniladi va tortishish gradient effektlari ahamiyatsiz boʻlsa, ogʻirlik markazi va massa markazi bir xil boʻladi va bir-birining oʻrnida ishlatiladi.
Fizikada massa taqsimotini modellashtirish uchun massa markazidan foydalanishning afzalliklarini uzluksiz tanadagi tortishish kuchlarining natijasini hisobga olgan holda koʻrish mumkin. Hajmning har bir nuqtasida r (r) zichligi V hajmli Q jismni koʻrib chiqaylik. Parallel tortishish maydonida har bir r nuqtadagi f kuchi quyidagicha ifodalanadi:
Bu yerda dm — r nuqtadagi massa, g — tortishish tezlashishi va — vertikal yoʻnalishni belgilovchi birlik vektor.
Ovoz hajmida mos yozuvlar nuqtasi R ni tanlang va shu nuqtada hosil boʻlgan kuch va momentni hisoblaymiz:
va
Agar R mos yozuvlar nuqtasi massa markazi boʻlishi uchun tanlansa, u holda
natijada olingan moment T = 0 ni bildiradi. Natijada paydo boʻlgan moment nolga teng boʻlganligi sababli, tana massasi massa markazida toʻplangan zarra kabi harakat qiladi.
Ogʻirlik markazini qattiq jism uchun mos yozuvlar nuqtasi sifatida tanlab, tortishish kuchlari tananing aylanishiga olib kelmaydi, yaʼni tananing ogʻirligi massa markazida toʻplangan deb hisoblash mumkin.
- ↑ Shore 2008.
- ↑ 2,0 2,1 2,2 2,3 Baron 2004.
- ↑ Mancosu 1999.
- ↑ Erlichson, H. (1996). "Christiaan Huygens' discovery of the center of oscillation formula". American Journal of Physics 64 (5): 571–574. doi:10.1119/1.18156. ISSN 0002-9505. https://aapt.scitation.org/doi/10.1119/1.18156.
- ↑ Walton 1855.
- ↑ Beatty 2006.
- ↑ Levi 2009.
- ↑ Bai & Breen 2008.
Manbalar[tahrir | manbasini tahrirlash]
- Asimov, Isaac (1988) [1966], Understanding Physics, Barnes & Noble Books, ISBN 978-0-88029-251-1
- Bai, Linge; Breen, David (2008). "Calculating Center of Mass in an Unbounded 2D Environment". Journal of Graphics, GPU, and Game Tools 13 (4): 53–60. doi:10.1080/2151237X.2008.10129266.
- Baron, Margaret E. (2004) [1969], The Origins of the Infinitesimal Calculus, Courier Dover Publications, ISBN 978-0-486-49544-6
- Beatty, Millard F. (2006), Principles of Engineering Mechanics, Volume 2: Dynamics—The Analysis of Motion, Mathematical Concepts and Methods in Science and Engineering, 33-jild, Springer, ISBN 978-0-387-23704-6
- De Silva, Clarence W. (2002), Vibration and shock handbook, CRC Press, ISBN 978-0-8493-1580-0
- Federal Aviation Administration (2007), Aircraft Weight and Balance Handbook (PDF), United States Government Printing Office, 19 October 2011da asl nusxadan (PDF) arxivlandi, qaraldi: 23 October 2011
- Feynman, Richard; Leighton, Robert B.; Sands, Matthew (1963), The Feynman Lectures on Physics, 1-jild (Sixth printing, February 1977-nashr), Addison-Wesley, ISBN 978-0-201-02010-6

























