Bessel funktsiyalari

Matematikadagi Bessel funktsiyalari — bu Bessel differentsial tenglamasining kanonik yechimlari boʻlgan funktsiyalar oilasidir:

$x^{2}{\frac {d^{2}y}{dx^{2}}}+x{\frac {dy}{dx}}+(x^{2}-\alpha ^{2})y=0,$

qayerda $\alpha$ ixtiyoriy haqiqiy son (umumiy holatda, kompleks son), tartib deb ataladi.

Eng koʻp ishlatiladigan Bessel funktsiyalari butun sonli tartiblarning funktsiyalaridir.

Garchi $\alpha$ va $(-\alpha )$ bir xil tenglamalarni yaratadi, ular odatda turli funktsiyalar ularga mos kelishiga rozi boʻlishadi (bu, masalan, Bessel funktsiyasida $\alpha$ silliq boʻlishi uchun amalga oshiriladi.).

Bessel funktsiyalari birinchi marta shveytsariyalik matematik Daniel Bernoulli tomonidan aniqlangan va Fridrix Bessel sharafiga nomlagan.

Ilovalar

Bessel tenglamasi silindrsimon va sferik koordinatalarda Laplas tenglamasi va Gelmgolts tenglamalarining yechimlarini topishda yuzaga kelib qoladi. Shuning uchun Bessel funktsiyalari toʻlqinlarning tarqalishi, statik potentsiallar va boshqalarning koʻplab muammolarini hal qilishda qoʻllaniladi, masalan:

• silindrsimon toʻlqin qoʻllanmada elektromagnit toʻlqinlar ;
• silindrsimon ob’ektlardagi issiqlik oʻtkazuvchanligi ;
• yupqa dumaloq membrananing toʻlqin shakllari;
• dumaloq tuynuk bilan diffraksiyalangan yorugʻlik intensivligini taqsimlash;
• suyuqlik bilan toʻldirilgan va oʻz oʻqi atrofida aylanadigan silindrdagi zarrachalarning tezligi;
• sferik simmetrik potentsial qutidagi toʻlqin funktsiyalari.

Bessel funktsiyalari boshqa muammolarni hal qilishda, masalan, signalarni qayta ishlashda ham qoʻllaniladi.

Bessel funksiyasi sinus funksiyasini umumlashtirilishidir. Bu oʻzgaruvchan qalinligi, oʻzgaruvchan kuchlanish (yoki ikkala shart bir vaqtning oʻzida) boʻlgan ipning tebranishi sifatida talqin qilinishi mumkin; oʻzgaruvchan xususiyatlarga ega boʻlgan muhitda tebranishlar; disk membranasining tebranishlari va boshqalarni oʻz ichiga oladi.

Taʼriflar

Yuqoridagi tenglama ikkinchi tartibli chiziqli differensial tenglama bo‘lgani uchun uning ikkita chiziqli mustaqil yechimi bo‘lishi kerak. Biroq, ushbu qarorlarning turli xil taʼriflari vaziyatga qarab tanlanadi. Quyida ulardan baʼzilari misol tariqasida keltirilgan.

Birinchi turdagi Bessel funktsiyalari

Belgilangan birinchi turdagi Bessel funktsiyalari $J_{\alpha }(x)$, yechimlar nuqtada cheklangan $x=0$ butun yoki manfiy boʻlmagan $\alpha$ uchun qoʻllaniladi . Muayyan funktsiyani tanlash va uni normallashtirish uning xususiyatlari bilan belgilanadi. Ushbu funktsiyalarni Teylor seriyasida nolga yaqin kengaytirish orqali aniqlash mumkin (yoki $\alpha$ butun sonlar uchun umumiy quvvat seriyasida):

$J_{\alpha }(x)=\sum _{m=0}^{\infty }{\frac {(-1)^{m}}{m!\,\Gamma (m+\alpha +1)}}{\left({\frac {x}{2}}\right)}^{2m+\alpha }.$

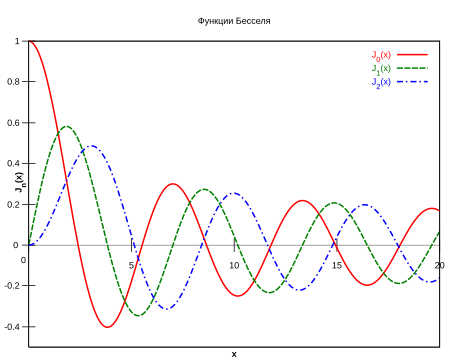
Bu yerda $\Gamma (z)$ Bu Eyler gamma funktsiyasi boʻlib, faktorialni butun son boʻlmagan qiymatlarga umumlashtirishdir. Bessel funktsiyasining grafigi sinusoidga oʻxshaydi, uning tebranishlari proportsional ravishda parchalanadi. ${\frac {1}{\sqrt {x}}}$, garchi aslida funktsiyaning nollari vaqti-vaqti bilan joylashmasa ham (ammo, ketma-ket ikkita nol orasidagi masofa $\pi$ da $x\to \infty$) .

Quyida jadvallar keltirilgan $J_{\alpha }(x)$ uchun $\alpha =0,1,2$ :

Birinchi turdagi Bessel funksiyasining grafigi J

Agar a $\alpha$ butun son emas, funktsiyalar $J_{\alpha }(x)$ va $J_{-\alpha }(x)$ chiziqli mustaqil va shuning uchun tenglamaning yechimlari shu boʻladi. Lekin agar $\alpha$ butun son boʻlsa, quyidagi munosabat toʻgʻri boʻladi:

$J_{-\alpha }(x)=(-1)^{\alpha }J_{\alpha }(x).$

Bu shuni anglatadiki, bu holda funktsiyalar chiziqli bogʻliqdir. Keyin tenglamaning ikkinchi yechimi ikkinchi turdagi Bessel funktsiyasi boʻladi (2-rasmga qarang). .

Bessel integrallari

Butun sonlar uchun Bessel funktsiyasining boshqa taʼrifini berish mumkin $\alpha$, integral yordamida koʻramiz:

$J_{\alpha }(x)={\frac {1}{\pi }}\int \limits _{0}^{\pi }\!\cos(\alpha \tau -x\sin \tau )\,d\tau .$

Bu yondashuv Bessel tomonidan qoʻllanilgan va u funksiyalarning baʼzi xususiyatlarini oʻrganish uchun foydalangan. Boshqa integral vakillik ham boʻlishi mumkin:

$J_{\alpha }(x)={\frac {1}{2\pi }}\int \limits _{-\pi }^{\pi }\!e^{i(\alpha \tau -x\sin \tau )}\,d\tau .$

Bessel funktsiyasining toʻliq boʻlmagan holda integral tasvirini topish $\alpha$ abtsissa oʻqi boʻylab kesma mavjudligini hisobga olish kerak. Buning sababi, integral endi yoʻq $2\pi$ — davriy. Shunday qilib, integratsiya konturi 3 qismga boʻlinadi: nur $-\infty$ dan $1$ gacha, qayerda ${\textstyle \varphi =-\pi }$, birlik radiusi doirasi va nur $1$dan $+\infty$gacha${\textstyle \varphi =\pi }$ . Oddiy matematik oʻzgarishlarni amalga oshirib, siz quyidagi integral tasvirni olishingiz mumkin:

$J_{\alpha }(x)={\frac {1}{2\pi }}\int \limits _{-\pi }^{\pi }\!e^{i(xsin(\varphi )-\alpha \varphi )}d\varphi -{\frac {\sin(\alpha \pi )}{\pi }}\int \limits _{1}^{\infty }{\frac {e^{-{\frac {1}{2}}x(r-{\frac {1}{r}})}}{{}r^{\alpha +1}}}dr.$

Butun son uchun buni tekshirish oson $\alpha$ bu ifoda oldingi formulaga qoʻyiladi.

Neyman funktsiyalari

Neyman funksiyalari — Yechimlar $Y_{\alpha }(x)$ Bessel tenglamalari bir nuqtada cheksiz boʻladi u nuqta $x=0$ .

Bu xususiyat bilan $J_{\alpha }(x)$ quyidagi nisbatga bogʻliq:

$Y_{\alpha }(x)={\frac {J_{\alpha }(x)\cos(\alpha \pi )-J_{-\alpha }(x)}{\sin(\alpha \pi )}},$

bu erda butun son boʻlsa $\alpha$ chegarasi olinadi $\alpha$, masalan, Lapital qoidasi yordamida hisoblangan.

Neyman funksiyalari ikkinchi turdagi Bessel funksiyalari deb ham ataladi. Birinchi va ikkinchi turdagi Bessel funktsiyalarining chiziqli birikmasi Bessel tenglamasining toʻliq yechimidir:

$y(x)=C_{1}J_{\alpha }(x)+C_{2}Y_{\alpha }(x).$

Quyida grafik keltirilgan $Y_{\alpha }(x)$ uchun $\alpha =0,1,2$ :

Ikkinchi turdagi Bessel funksiyasining grafigi N

Bir qator kitoblarda Neyman funktsiyalari koʻrsatilgan $N_{\alpha }(x)$ .

Sferik Bessel funktsiyalari

Birinchi turdagi sferik Bessel funktsiyalari,j_n(x), uchunn = 0, 1, 2

Ikkinchi turdagi sferik Bessel funktsiyalari,y_n(x), uchunn = 0, 1, 2

Sferik koordinatalarda Helmgolts tenglamasini oʻzgaruvchilarni ajratish usuli bilan yechishda radial qism uchun tenglama shaklga ega boʻladi.

$x^{2}{\frac {d^{2}y}{dx^{2}}}+2x{\frac {dy}{dx}}+\left(x^{2}-n(n+1)\right)y=0.$

Ikkinchi chiziqli mustaqil yechim sferik Bessel funksiyalari deyiladi j_n va y_n va odatiy Bessel funktsiyalari bilan bogʻliq J_n va Neyman Y_n yordamida ifodalanadi.

${\begin{aligned}j_{n}(x)&={\sqrt {\frac {\pi }{2x}}}J_{n+{\frac {1}{2}}}(x),\\y_{n}(x)&={\sqrt {\frac {\pi }{2x}}}Y_{n+{\frac {1}{2}}}(x)=(-1)^{n+1}{\sqrt {\frac {\pi }{2x}}}J_{-n-{\frac {1}{2}}}(x).\end{aligned}}$

y_n ham n_nyoki η_n bilan belgilanadi; baʼzi mualliflar bu funktsiyalarni sferik Neyman funktsiyalari deb atashadi.

Sferik Bessel funksiyalarini (Reyleigh formulasi) shaklida ham yozish mumkin boʻladi.

${\begin{aligned}j_{n}(x)&=(-x)^{n}\left({\frac {1}{x}}{\frac {d}{dx}}\right)^{n}{\frac {\sin x}{x}},\\y_{n}(x)&=-(-x)^{n}\left({\frac {1}{x}}{\frac {d}{dx}}\right)^{n}{\frac {\cos x}{x}}.\end{aligned}}$

Bir necha birinchi sharsimon Bessel funksiyalari dan misollar :

${\begin{aligned}j_{0}(x)&={\frac {\sin x}{x}},\\j_{1}(x)&={\frac {\sin x}{x^{2}}}-{\frac {\cos x}{x}},\\j_{2}(x)&=\left({\frac {3}{x^{2}}}-1\right){\frac {\sin x}{x}}-{\frac {3\cos x}{x^{2}}},\\j_{3}(x)&=\left({\frac {15}{x^{3}}}-{\frac {6}{x}}\right){\frac {\sin x}{x}}-\left({\frac {15}{x^{2}}}-1\right){\frac {\cos x}{x}}\end{aligned}}$

va Neyman :

${\begin{aligned}y_{0}(x)&=-j_{-1}(x)=-{\frac {\cos x}{x}},\\y_{1}(x)&=j_{-2}(x)=-{\frac {\cos x}{x^{2}}}-{\frac {\sin x}{x}},\\y_{2}(x)&=-j_{-3}(x)=\left(-{\frac {3}{x^{2}}}+1\right){\frac {\cos x}{x}}-{\frac {3\sin x}{x^{2}}},\\y_{3}(x)&=j_{-4}(x)=\left(-{\frac {15}{x^{3}}}+{\frac {6}{x}}\right){\frac {\cos x}{x}}-\left({\frac {15}{x^{2}}}-1\right){\frac {\sin x}{x}}.\end{aligned}}$

Funktsiyalarni keltirib chiqarish

Sferik Bessel funksiyalarini yaratish :

${\begin{aligned}{\frac {1}{z}}\cos \left({\sqrt {z^{2}-2zt}}\right)&=\sum _{n=0}^{\infty }{\frac {t^{n}}{n!}}j_{n-1}(z),\\{\frac {1}{z}}\sin \left({\sqrt {z^{2}-2zt}}\right)&=\sum _{n=0}^{\infty }{\frac {t^{n}}{n!}}y_{n-1}(z).\end{aligned}}$

Differentsial munosabatlar

Quyidagi formulalardaf_n bilan almashtirilishi mumkinj_n ,y_n h(1)n, h(1)n, h(2)n, h(2) sharsimon Hankel funktsiyalari, uchunn = 0, ±1, ±2, … :

${\begin{aligned}\left({\frac {1}{z}}{\frac {d}{dz}}\right)^{m}\left(z^{n+1}f_{n}(z)\right)&=z^{n-m+1}f_{n-m}(z),\\\left({\frac {1}{z}}{\frac {d}{dz}}\right)^{m}\left(z^{-n}f_{n}(z)\right)&=(-1)^{m}z^{-n-m}f_{n+m}(z).\end{aligned}}$

Xususiyatlari

Ortogonallik

Mayli $\mu _{1},\mu _{2}$ Bessel funksiyasining nollari $J_{\alpha }(x)$ . Keyin :

$\int _{0}^{1}{xJ_{\alpha }(\mu _{1}x)J_{\alpha }(\mu _{2}x)dx}=\left\{{\begin{matrix}0&{\mbox{;}}\quad \mu _{1}\neq \mu _{2}\\\\{\frac {1}{2}}(J'_{\alpha }(\mu _{1}))^{2}&{\mbox{;}}\quad \mu _{1}=\mu _{2}\end{matrix}}\right.$ .

Asimptotiklar

Asimptotik formulalar birinchi va ikkinchi turdagi Bessel funktsiyalari uchun maʼlum. Kichik argumentlar uchun $(0<x\ll {\sqrt {\alpha +1}})$ va haqiqiy $\alpha$ ular shunday koʻrinadi :

$J_{\alpha }(x)\rightarrow {\frac {1}{\Gamma (\alpha +1)}}\left({\frac {x}{2}}\right)^{\alpha },$

$Y_{\alpha }(x)\rightarrow \left\{{\begin{matrix}{\frac {2}{\pi }}\left[\ln(x/2)+\gamma \right]&{\mbox{;}}\quad \alpha =0\\\\-{\frac {\Gamma (\alpha )}{\pi }}\left({\frac {2}{x}}\right)^{\alpha }&{\mbox{;}}\quad \alpha >0\end{matrix}}\right.$ ,

qayerda $\gamma$ — Eyler doimiysi — Mascheroni (0,5772 …) va $\Gamma$ Eyler gamma funktsiyasidir . Katta argumentlar uchun ($x\gg |\alpha ^{2}-1/4|$) formulalar quyidagichakoʻrinishda koʻrinadi:

$J_{\alpha }(x)\rightarrow {\sqrt {\frac {2}{\pi x}}}\cos \left(x-{\frac {\alpha \pi }{2}}-{\frac {\pi }{4}}\right),$

$Y_{\alpha }(x)\rightarrow {\sqrt {\frac {2}{\pi x}}}\sin \left(x-{\frac {\alpha \pi }{2}}-{\frac {\pi }{4}}\right).$

Asimptotik kengayishning keyingi atamasidan foydalanish natijani sezilarli darajada yaxshilash imkonini beradi. Nolinchi tartibli Bessel funktsiyasi uchun u quyidagicha koʻrinishda koʻrinadi:

$J_{0}\rightarrow {\sqrt {\frac {2}{\pi x}}}\cos(x-{\frac {\pi }{4}})+{\frac {1}{4x{\sqrt {2\pi x}}}}\sin(x-{\frac {\pi }{4}}).$

Gipergeometrik qatorlar

Bessel funktsiyalari gipergeometrik funktsiya bilan ifodalanishi mumkin:

$J_{\alpha }(z)={\frac {(z/2)^{\alpha }}{\Gamma (\alpha +1)}}{}_{0}F_{1}(\alpha +1;-z^{2}/4).$

Shunday qilib, butun son uchun $\alpha$ Bessel funktsiyasi bitta qiymatli analitikdir va butun sonlar uchun u koʻp qiymatli analitik boʻladi.

Yaratish funktsiyasi

Birinchi turdagi Bessel funktsiyalari va maʼlum bir turdagi funktsiyaning Loran qatori koeffitsientlari boʻyicha butun tartibli tasvirlar mavjuddir.

$e^{{\frac {z}{2}}\left(w-{\frac {1}{w}}\right)}=\sum _{n=-\infty }^{+\infty }J_{n}(z)w^{n}.$

Nisbatlar

Yakobi-Angera formulasi va tegishli

Hosil qiluvchi funksiya ifodasidan olingan $a=1$, $w=e^{i\phi }$ :

$e^{iz\sin \phi }=J_{0}(z)+2\sum _{n=1}^{\infty }J_{2n}(z)\cos(2n\phi )+2i\sum _{n=1}^{\infty }J_{2n-1}(z)\sin(2n-1)\phi .$

$a=1$, $t=ie^{i\phi }$da :

$e^{iz\cos \phi }=J_{0}(z)+2\sum _{n=1}^{\infty }i^{n}J_{n}(z)\cos(n\phi ).$

Takroriy munosabatlar

Bessel funksiyalari uchun bir qancha takrorlanish munosabatlari mavjuddir. Mana ulardan baʼzilari quyidagilar:

$J_{\alpha +1}={\frac {\alpha }{x}}J_{\alpha }-J'_{\alpha }(x);$

$J_{\alpha +1}(x)+J_{\alpha -1}(x)={\frac {2\alpha }{x}}J_{\alpha }(x);$

$J_{\alpha +1}(x)-J_{\alpha -1}(x)=-2J'_{\alpha }(x)$ .

Qoʻshish teoremasi

Har qanday butun n va kompleks uchun $z_{1}$, $z_{2}$ bajarilgan

$J_{n}(z_{1}+z_{2})=\sum _{k=-\infty }^{\infty }J_{k}(z_{1})J_{n-k}(z_{2}).$

Integral ifodalar

Har qanday masala uchun $a$ va $b$ (shu jumladan murakkab) uchun quyidagilar bajarildi

$\int _{0}^{\infty }e^{-at}J_{n}(bt)\mathrm {d} t={\frac {b^{n}}{{\sqrt {a^{2}+b^{2}}}({\sqrt {a^{2}+b^{2}}}+a)^{n}}}.$

Oxirgi formulaning alohida holati ifodadir

$\int _{0}^{\infty }e^{-at}J_{0}(bt)\mathrm {d} t={\frac {1}{\sqrt {a^{2}+b^{2}}}}.$

Shuningdek

• Silindrsimon funktsiyalar
• Sferik funktsiyalar
• Oʻzgartirilgan Bessel funktsiyalari
• Bessel nuri

Adabiyotlar

• Ватсон Г. . Теория бесселевых функций. М.: ИЛ, 1949. 
• Бейтмен Г., Эрдейи А.  „Функции Бесселя, функции параболического цилиндра, ортогональные многочлены“,. Высшие трансцендентные функции. Т. 2. 2-е изд. М.: Наука, 1974. 
• Лаврентьев М. А., Шабат Б. В. . Методы теории функций комплексного переменного. М.: Наука, 1973.